
EN TIERRA NUEVA

1.- LOS CONSTRUCTORES DE LA CATEDRAL
En el mundo del átomo y sus componentes, todo aparece en montones (quantum = cuanto = montón). La masa, la energía, el momento, etc., aparece en montones: nada en este mundo es liso y continuo. Mecánica es el antiguo término para la Ciencia del movimiento, así que Mecánica Cuántica es la rama de la Ciencia dedicada a describir el movimiento de las cosas en el mundo subatómico. Mott la define como la rama de la Física que describe el comportamiento de los electrones en los átomos, en las moléculas y en los sólidos o también como la rama de la Física matemática que permite calcular las propiedades de los átomos. Sin embargo es algo más que eso:
la Mecánica Cuántica proporciona el soporte fundamental de toda la Ciencia moderna; sus ecuaciones describen el comportamiento de objetos a escala atómica, proporcionando la única explicación del mundo de lo minúsculo. Sin sus ecuaciones, los científicos no habrían sido capaces de diseñar centrales o bombas nucleares, construir láseres, explicar por qué el Sol se mantiene caliente, la Química estaría aún en una época oscura y no existiría la biología molecular, la comprensión del DNA, la ingeniería genética, etc.,etc.,etc.
El mayor problema que tenemos a la hora de ocuparnos de la Mecánica Cuántica procede de nuestra suposición inconsciente de que las cosas se comportarán del mismo modo en el mundo cuántico que como lo hacen en el mundo normal de nuestra experiencia. No hay ninguna razón para esperar que cuando contemplamos objetos muy pequeños u objetos muy veloces, éstos se comporten de la misma forma que lo hacen los objetos con los que estamos familiarizados. La Física Cuántica representa una de las conquistas fundamentales de la Ciencia, mucho más significativa y directa, desde el punto de vista práctico, que la Teoría de la Relatividad.
En su mundo, las leyes habituales de la Física dejan de funcionar: los acontecimientos pasan a estar gobernados por probabilidades. La Relatividad y la Mecánica Cuántica constituyen las teorías básicas de la Física moderna; independientemente del grupo de Gotinga, Dirac descubrió que las ecuaciones de la Mecánica Cuántica tienen la misma estructura matemática que las ecuaciones de la Mecánica clásica, y que ésta es un caso particular de la Cuántica correspondiente a grandes números cuánticos o a dar el valor 0 a la constante de Plank.
La Mecánica Cuántica es como una catedral que se levanta dentro del gran edificio de la Física, de la Ciencia entera. Su construcción arranca con la genial idea de un fundador, Max Plank, un gran seguidor, Bohr, un revolucionario, De Broglie, unos padres, Schroedinger y Heisenberg, un gran matemático, Dirac, y muchos continuadores. Conozcamos, aunque sea brevemente, las biografías de algunos de estos científicos.
1.-1.- MAX PLANK
Físico alemán nacido en Kiel, Schleswig, el 23 de abril de 1858 y muerto en Gotinga, el 3 de octubre de 1947. La familia de Plank se trasladó a Munich cuando Max era todavía un niño, y allí recibió su primera enseñanza. En los tiempos universitarios se fue a Berlín, en donde tuvo de profesores a Helmholtz y Kirchhoff. En 1885 fue profesor en la Universidad de Kiel, y en 1889, en Berlín, donde permaneció hasta su retiro en 1926. El trabajo doctoral de Plank versó sobre Termodinámica; en particular se fijó en el problema del cuerpo negro, que absorbe todas las frecuencias de la luz y por eso cuando se calienta las emite.
En 1900 consiguió una ecuación muy simple que describía con precisión la distribución de irradiación de las variadas frecuencias; se basaba en una suposición decisiva: la energía no es divisible indefinidamente. Como la materia, estaba formada por partículas, a las que llamó cuantos, siendo el tamaño de cada uno, para cada radiación electromagnética, directamente proporcional a su frecuencia. A la pequeña constante de proporcionalidad se la llamó, en su honor, constante de Plank, y se reconoce ahora como una de las constantes fundamentales del Universo.
Esta teoría era tan revolucionaria que ni el mismo Plank creía completamente en ella, sospechando que podía ser una trampa matemática sin ninguna relación con algo real. Pero cuando Einstein la aplicó al efecto fotoeléctrico y Bohr al modelo atómico con tan excelentes resultados, la teoría cuántica había alcanzado tanta importancia que Plank recibió el Nobel en 1918. En 1930, Plank fue nombrado presidente de la Sociedad Kaiser Guillermo, de Berlín, que por él recibió el nombre de Sociedad de Max Plank. En su ancianidad, su celebridad sólo fue superada por la de Einstein; se opuso a Hitler y no prestó ni su prestigio ni su opinión al régimen, viéndose forzado a dimitir de la presidencia de la Sociedad en 1937. Fuerzas americanas le rescataron en 1945 durante los últimos días de confusión antes de la derrota final alemana.
Le nombraron de nuevo presidente de la Sociedad hasta encontrarle un sucesor y le trasladaron a Gotinga, donde pasó sus dos últimos años estimado y respetado.
1.-2.- NIELS BOHR
Físico danés nacido en Copenhague el 7 de octubre de 1885 y muerto en la misma ciudad el 18 de noviembre de 1962. Hijo de un profesor de Fisiología, estudió Física en la Universidad de Copenhague, donde también destacó como un gran jugador de fútbol. Trabajó en Cambridge con Rutherford, volviendo en 1916 a la Universidad de Copenhague como profesor de Física. En 1913 ya tenía ideado su modelo del átomo, que fue el primer intento razonable y con éxito para explicar el espectro de un elemento a partir de la estructura interna de dicho átomo, y usar los datos espectrocópicos para explicar la estructura interna del átomo, utilizando las ideas cuánticas de Plank. Fue incapaz de desarrollar modelos atómicos satisfactorios de elementos más complejos que el hidrógeno, y su modelo primitivo fue perfeccionado por otros científicos, aunque siempre quedó como un híbrido cuantico-clásico. Mantuvo un interminable debate con Einstein sobre los principios de la Mecánica Cuántica, de la que fue un convencido defensor, y los hechos científicos acabaron dándole la razón.
En 1940, las tropas de Hitler invadieron Dinamarca, y para evitar ser encarcelado (no cooperó en la ocupación), huyó a Inglaterra, y posteriormente a Estados Unidos, donde intervino en el proyecto de la bomba atómica de Los Alamos, hasta 1945. Trabajó incansablemente en favor del desarrollo de la energía atómica para usos pacíficos, organizando la primera Conferencia de Atomos para la Paz en Ginebra.
1.-3.- ERWIN SCHROEDINGER
Físico austríaco nacido en Viena en 1887 y muerto en Viena en 1961. Estudia en la Universidad de Viena anteriormente a la Primera Guerra Mundial, durante la cual fue oficial de artillería en el frente del Sudoeste. Después de la guerra marchó a Alemania, y en 1921 era profesor en la Universidad de Stuttgart. Al conocer la teoría onda- corpúsculo de De Broglie, pensó en introducirla en el modelo atómico de Bohr. En su modelo atómico, el electrón puede estar situado en cualquier órbita alrededor de la cual sus ondas pueden proyectarse en un número exacto de longitudes de onda, produciendo este fenómeno una onda estacionaria; mientras el electrón permanecía en su órbita, no precisaba de luz radiante y de ese modo no violaba las ecuaciones de Maxwell. Más aún, cualquier órbita situada entre dos posibles, donde se requiera un número fraccionario de longitud de onda, no es posible, lo que lleva a la conclusión de órbitas separadas como consecuencia de las propiedades del electrón y no como mera deducción arbitraria de las líneas espectrales.
Junto con otros científicos, como Dirac y Born, desarrolló la base matemática relacionada con el concepto anterior, construyendo la Mecánica Cuántica sobre la teoría de Plank un cuarto de siglo después de su promulgación, siendo el punto clave la ecuación de onda de Schroedinger. Su trabajo se publicó en 1926, demostrándose posteriormente que la mecánica matricial de Heisenberg, publicada en 1925, era equivalente a la suya. Por ello recibió el Nobel en 1933, compartiéndolo con Dirac. En 1928 haba sucedido a Plank como profesor de Física en la Universidad de Berlín, pero al subir Hitler al poder, marchó a Austria, y de ahí, a Inglaterra, en 1938, al ser absorbido su país por Alemania. En 1940 fue nombrado profesor en Dublín, donde le siguió Dirac, su compañero de fatigas en la Mecánica ondulatoria. En 1956 volvió a Viena, donde vivió el resto de su vida.
1.-4.- MAX BORN
Físico alemán-británico, nacido en Breslau, Silesia, (actualmente Wroclaw, Polonia), en 1882, y muerto en Gotinga en 1970. Dedicó su obra principal a forjar las bases matemáticas de la Mecánica Cuántica. Dio una interpretación probabilista al electrón-onda: el aumento y la disminución de las ondas se podía tomar de modo que indicaran el aumento y la disminución de la probabilidad de que el electrón se comportara como si existiera en puntos específicos del paquete de ondas.
Igual que Schroedinger, Born se marchó de Alemania en cuanto Hitler subió al poder, yéndose a Cambridge en 1933. Allí fue profesor de Física matemática en la Universidad de Edimburgo en 1936, convirtiéndose en ciudadano británico en 1939. Después de su retiro en 1953 volvió a Alemania, y en 1954 fue recompensado con el premio Nobel de Física por sus trabajos sobre Mecánica Cuántica, compartiéndolo con Bothe.
1.-5.- LOUIS DE BROGLIE
Físico francés nacido en Dieppe, Seine- Marne, el 15 de agosto de 1892 y muerto en 1987. Procedió de familia aristocrática francesa, muriendo su tatarabuelo durante la Revolución, en la guillotina. Recibió su enseñanza en la Sorbona y fue después de la Primera Guerra Mundial, donde sirvió como especialista de radio, cuando empezó a interesarse por la Física teórica. En 1924 obtuvo su doctorado por una tesis relacionada con la Mecánica Cuántica, aunque fue el año anterior cuando llevó a cabo su gran hazaña.
Por una simple combinación de la fórmula de Einstein y la de Plank, demostró que cada partícula debe tener una onda asociada a ella. Las longitudes de dichas ondas, que no son de naturaleza electromagnética y que recibieron el nombre de ondas de materia, están relacionadas inversamente con el momento de la partícula. Para un cuerpo grande, la onda es indetectable, pero para uno pequeñísimo, como el electrón, la longitud de su onda asociada tendría la magnitud aproximada a los rayos X, y, por tanto, se podía detectar (fueron detectadas por Davisson y G.P.Thomson en 1927).
Este dualismo onda-corpúsculo del electrón coincidía con el del fotón, demostrado por Compton. Schroedinger usó el nuevo concepto de onda para construir un modelo del átomo en el cual los electrones en movimiento de Bohr daban lugar a ondas electrónicas estacionarias. De manera similar, los electrones estáticos de Lewis, producían, en conexión con la formación del enlace químico, las ondas electrónicas en resonancia de Pauling. Por sus trabajos en la dualidad onda- corpúsculo recibió el Nobel en 1929, y desde 1945 hasta su fallecimiento fue asesor técnico de la comisión francesa de energía atómica.
1.-6.- WOLFGANG PAULI
Físico austríaco-americano nacido en Viena en 1900 y muerto en Zurich, Suíza, en 1958. Estudió bajo la supervisión de Sommerfeld en la Universidad de Munich y obtuvo su doctorado en 1921. Después de efectuar trabajos de post-doctorado con Bohr, entró a formar parte del profesorado de la Universidad de Hamburgo en 1923. En 1925 anunció su Principio de Exclusión; había admitido la inclusión de un nuevo número cuántico a la teoría de Bohr- Sommerfeld, y postulado que un electrón no puede tener los cuatro números cuánticos iguales a otro. Por este trabajo recibió, tardíamente, el Nobel en 1945.
En 1931 sugirió que cuando se emitía una partícula β (electrón acelerado) por un átomo, se emitía también otra partícula sin carga y quizás sin masa, que era la responsable de la energía que faltaba, ya que era un hecho comprobado que las partículas beta tenían menos energía de la debida, lo que contradecía el principio de conservación; al año siguiente, Fermi dio el nombre de neutrino a la partícula postulada por Pauli, que en italiano significa pequeña cosa neutra. Hasta 1956 no pudo ser detectado el neutrino. Durante los años 30, Pauli fue a menudo a los Estados Unidos, y al llegar la guerra se quedó allí permanentemente, nacionalizándose en 1946.
1.-7.- LINUS PAULING
Químico americano nacido en Portland, Oregón, en 1901. Estudió en la Universidad de Oregón, graduándose en 1922. Obtuvo el doctorado en el California Institute of Technology y desde entonces fue profesor de dicha institución. Desarrolló una teoría, basándose en la Mecánica Cuántica, sobre estructura molecular, mediante la cual los electrones, considerados como ondas, actuaban en pares para dar lugar a un sistema menos energético y más estable que al actuar independientemente. Una combinación de este tipo sólo podía tener lugar si los átomos de los cuales formaban parte los electrones, permanecían próximos unos a otros. De este modo el enlace químico entre los átomos empezó a explicarse, y muchas de las cosas que habían sido misteriosas en la Química Orgánica y que se habían aceptado como hechos empíricos, podían ahora demostrarse racionalmente según las ideas de Pauling.
Demostró posteriormente la teoría de la resonancia debido a que los electrones-onda eran "desparramados" a lo largo de una región relativamente extensa, explicando las propiedades del benceno y haciendo posible la realización de muchos otros trabajos que de otra manera no hubieran podido llevarse a cabo. En los años 50 fue el primero en sugerir que las moléculas proteicas tenían forma de hélice, produciendo un gran impacto en el campo de la Genética; en 1954 recibió el Nobel de Química por sus trabajos en estructura molecular y en 1963 el de la Paz, por su lucha contra el peligro nuclear: junto a Marie Curie, ha sido la única persona en recibir dos premios Nobel.
1.-8.- WERNER HEISENBERG
Físico alemán nacido en Duisburgo en 1901 y muerto en 1976. Estudió con Sommerfeld en la Universidad de Munich, obteniendo su doctorado en 1923. Trabajó como ayudante de Born en Gotinga y con Bohr en Copenhague. Interesado por el modelo atómico, no era partidario de concebir imágenes, sino relegarse a los fenómenos observables y no a las figuras imaginarias, siguiendo la línea del pensamiento de Mach medio siglo antes.
Estudió las líneas espectrales, tratando de encontrar una relación matemática que las explicara, para lo cual, en 1927, utilizó el álgebra matricial en un sistema que llamó mecánica matricial y que consistía en un conjunto de cantidades que, correctamente manejadas, daban las longitudes de onda de las líneas espectrales. Este sistema era equivalente a la Mecánica Ondulatoria de Schroedinger, postulada meses después, que era más visual que la de Heisenberg, por lo que fue preferida por los físicos.
Los estudios de Heisenberg sobre teoría nuclear le condujeron a predecir que la molécula de hidrógeno podía existir en dos formas, teoría que se confirmó en 1929. Otra deducción, sorprendente y capital, fue el Principio de Indeterminación, que establece que es imposible realizar una determinación exacta y simultánea de la posición y del momento de un cuerpo; al multiplicar ambas indeterminaciones se obtenía la constante de Plank. Este principio debilitó la ley de la causa y el efecto, que había supuesto un áncora de la Ciencia, incuestionable desde la época de Tales; destruyó la filosofía determinista del Universo. Por este principio recibió el Nobel en 1932. Durante la Segunda Guerra mundial se encargó de la investigación alemana sobre la bomba atómica, pero antes de alcanzar su propósito terminó la guerra. Heisenberg, que era director del Instituto Max Plank de Berlín, fue nombrado director del mismo Instituto en Gotinga, después de la guerra.
1.-9.- PAUL DIRAC
Físico inglés nacido en Bristol, Gloucestershire, en 1902 y muerto en 1984. Estudió ingeniería eléctrica en la Universidad de Bristol, pero cambió de idea dedicándose a las matemáticas después de graduarse. Obtuvo su doctorado en la Universidad de Cambridge en 1926, haciendo de sí mismo un físico matemático. En 1932 ya era profesor lucasiano de matemáticas en Cambridge. Al final de los años 20, Dirac desarrolló de manera más precisa que Schroedinger, los estudios matemáticos iniciados por De Broglie sobre la dualidad onda-corpúsculo, explicando cómo a todas las partículas se les podía asociar una onda, y, por tanto, dando un gran impulso a la Mecánica Cuántica.
Ciertas ecuaciones propuestas por Dirac indicaban la existencia de antipartículas, antielectrones y antiprotones, con igual masa y carga pero diferente signo que sus homólogas. A pesar que esta teoría resultaba extravagante, fue rápidamente confirmada por Anderson al descubrir el antielectrón o positrón dos años más tarde, y por Segrè, al descubrir el antiprotón 25 años más tarde. Dirac había descubierto con sus ecuaciones la antimateria, abriendo la puerta a tierra desconocida en el mundo de la Física. Por sus trabajos en Mecánica Cuántica y antipartículas recibió el Nobel en 1933, junto a Schroeinger, y en 1940 fue nombrado profesor del Dublín Institute for Advances Studies. Teórico extraordinariamente bien dotado, su libro "Los principios de la Mecánica Cuántica" es una obra ya clásica que corrobora la categoría de su autor, quien hoy es considerado por la mayoría de los físicos como el Newton del siglo XX.
1.-10.- NEVILL MOTT
Físico inglés nacido en 1905, descubridor de los diferentes aspectos que ofrecen la estructura de los materiales desordenados. Estudio matemáticas en Cambridge y trabajó al lado de Rutherford. Posteriormente se trasladó a Copenhague, donde se unió al equipo de Bohr. En colaboración con H.Massey, aplicó la nueva MecánicaCuántica a la difusión de partículas en el campo de la Física atómica que él mismo creó. A los 28 años se trasladó a Bristol, donde bajo la influencia de H.Jones comenzó a interesarse por la Física del estado sólido. En 1954 pasó a ocupar la cátedra Cavendish, comenzando a trabajar sobre la transición entre el comportamiento de los metales y el de los aislantes (Transición de Mott). Fue Nobel en 1977.
1.-11.- RICHARD FEYNMAN
Físico americano nacido en Nueva York en 1918 y muerto en 1988. Se graduó en el Instituto de Tecnología de Massachusetts en 1939 y se doctoró en Princeton en 1942. Como todos los físicos de su generación, estuvo involucrado en las investigaciones de la bomba nuclear y presenció la explosión de la primera en Alamogordo. En 1945 ingresó en la Universidad de Cornell y en 1950 marchó al Instituto de Tecnología de California. A finales de los años 40 desarrolló la Electrodinámica cuántica, en la que se determinaba matemáticamente el comportamiento de los electrones con una precisión mucho mayor que la conseguida hasta entonces; por este trabajo obtuvo el Nobel en 1965, junto a Schwinger y Tomonaga, que también desarrollaron el mismo estudio de manera independiente.
Feynman fue una de las figuras más pintorescas de la Física contemporánea; solía entusiasmarse con todo tipo de rompecabezas y enigmas y disfrutaba de la compañía de personas de la más variada condición. Era conocido por las historias que relataba, sus frecuentes bromas sobre detalles triviales de la vida cotidiana y su afición a los jeroglíficos mayas, a abrir cajas de seguridad, tocar los bongos, dibujar, los experimentos de biología y la ciencia computacional.
1.-12.- ERNST JORDAN
Físico teórico alemán, nacido en 1902, considerado como unos de los fundadores de la Mecánica Cuántica. Creció y cursó estudios superiores en Hannover, trasladándose más tarde a Gotinga para hacer el doctorado. Tras conseguir una plaza en la Universidad de Rostock en 1929, se convirtió en profesor de Física de la misma en 1935. A continuación ganó las cátedras de Física de Berlín y Hamburgo. A los 23 años, Jordan colaboró con Born y más tarde con Heisenberg en orden a establecer los fundamentos de la teoría de la Mecánica Cuántica mediante el empleo del cálculo matricial (1926). Posteriormente contribuyó al avance de la Mecánica Cuántica de las interacciones entre electrones y fotones, denominada Electrodinámica cuántica, cuando esta teoría aún se hallaba en sus primeras fases de desarrollo. Otro campo en que Jordan publicó investigaciones de gran interés fue en el de la gravitación.
1.-13.- STEVEN WEINBERG
Físico norteamericano nacido en 1933, que construyó una teoría unificada del electromagnetismo y de la interacción nuclear débil. Hijo de un taquígrafo de juzgado, Weinberg se formó en las Universidades de Cornell y Princeton. Ocupó diversos puestos en Columbia, Berkeley, MIT y Harvard antes de convertirse en profesor de Física en Texas en 1986.
En 1967 había dado origen a la teoría gauge, que tiene que ver con cambios de marco de referencia. Basándose en ella, predijo correctamente tanto la fuerza nuclear débil como la fuerte (ambas ligadas a la desintegraciónnuclear), a pesar de que difieren en un factor de 10 10. De la teoría mencionada se deriva otra nueva interacción debida a la existencia de corrientes neutras a través de las cuales se produce el intercambio de una partícula sin carga con la consiguiente aparición de una fuerza entre las partículas. Tal predicción obtuvo su confirmación experimental en 1973, por lo que la teoría Weinberg-Salam goza de una sólida evidencia. Fue Nobel con Salam y Glashow en 1979.
1.-14.- ROGER PENROSE
Físico teórico inglés nacido en 1931. Su labor investigadora ha aumentado considerablemente nuestro conocimiento sobre la gravitación, sumándose a los esfuerzos emprendidos en nuestro siglo para formular una teoría cuántica de la gravedad. Hijo de un genetista experto en enfermedades mentales, Penrose estudió en el University College de Londres y en Cambridge. En 1966 era profesor de matemáticas aplicadas en el Birkbeck College londinense y en 1973, catedrático Rouse Ball de matemáticas de Oxford.
Al igual que Hawking, ha desvelado muchas de las propiedades de los agujeros negros. Penrose y Hawking demostraron la aparición de una singularidad espacio-temporal en el centro de un agujero negro, y Penrose estableció que los horizontes de sucesos nos impiden la observación de tales singularidades desde el exterior.
1.-15.- STEPHEN HAWKING
Físico teórico inglés nacido en 1942, que mejoró nuestra comprensión del espacio-tiempo y de las singularidades espacio-temporales. Obtuvo su licenciatura en Oxford y su doctorado en Cambridge, con una tesis sobre la teoría de la Relatividad. En 1979 ya era profesor lucasiano de matemáticas. Comenzó su carrera investigando sobre la Relatividad General, estableciendo que la teoría de Einstein no toma en cuenta la naturaleza mecánico-cuántica de la Física, de modo que no es adecuada para la descripción de singularidades gravitacionales tales como los agujeros negros o el mismo Big Bang. En 1973 mostraba que una singularidad espacio-temporal debió de estar presente en el comienzo del Universo, aunque posteriormente muestra un Universo sin singularidades. Penetró en el conocimiento de los agujeros negros, y en 1974 llegó a la conclusión que éstos emiten radiación térmica. Recientemente ha intentado producir una teoría de la gravedad consistente, dentro del marco de la Mecánica Cuántica. Murió en 2018, a los 76 años de edad
1.-16.- MURRAY GELL-MANN
Físico teórico norteamericano nacido en 1929, que aplicó la teoría de los grupos a la interpretación de las partículas elementales. Estudió en Yale y en el MIT, finalizando su doctorado a los 22 años. Trabajó con Fermi y en 1965 obtuvo la cátedra de Física teórica en el Instituto de Tecnología de California. Contribuyó extraordinariamente al estudio de las partículas elementales, introduciendo el concepto de quark, así como utilizó, junto a Feynman, las corrientes a la hora de interpretar y comprender la interacción débil. Fue Nobel en 1969.
2.- MAS ALLA DE LA FISICA CLASICA
A finales del siglo XIX, la Física era un Edificio, en apariencia, sólido, definitivo y terminado. Estaba basada entres pilares fundamentales, construídos por tres científicos que habían diseñado el edificio con una maestría sin igual: Galileo (1564-1642), Newton (1642-1727) y Maxwell (1831-1879).
Galileo, considerado el creador del Método Científico, lo aplicó en sus estudios sobre el movimiento de los cuerpos y en la defensa del sistema copernicano o teoría heliocéntrica del movimiento planetario. Newton, quizás el más grande científico de todos los tiempos, postuló y aplicó los conceptos básicos de la dinámica, aparte de otras amplísimas aportaciones a la Ciencia, como el cálculo infinitesimal y los estudios sobre gravitación y óptica.
Maxwell sistematizó el estudio de los fenómenos eléctricos y magnéticos en su obra "Tratado de electricidad y magnetismo", donde obtuvo las ecuaciones del campo electromagnético en la forma en que hoy son estudiadas, después de 100 años de su formulación original.
Pero a finales de siglo, ciertos experimentos no consiguen ser explicados por la Física clásica: el experimento de Michelson y Morley, el concepto de electrón, el efecto fotoeléctrico, los rayos X, las series espectrales, la radiación de incandescencia, la radiactividad, etc...todo ello prepara la revolución científica que tendría lugar a partir del año 1900.
Es precisamente en ese año, al comienzo del siglo XX, cuando Max Plank (1858-1947) publica sus resultados sobre las características de los espectros que emiten los cuerpos incandescentes, introduciendo la idea no clásica de que únicamente puede emitirse energía de forma discontinua o discreta, mediante múltiplos enteros de cuantos o paquetes elementales de energía: "Quantum", de donde deriva cuanto, es una palabra latina que significa "mucho" o "montón".
La idea de cuantización representó el paso decisivo hacia la nueva Física. Así, en 1905, Einstein (1879-1955), explicó con breve elegancia las leyes del efecto fotoeléctrico a partir de las ideas de Plank y de su célebre ecuación
E = h · f
donde E es la energía de la partícula, h una constante llamada, en su honor, constante de Plank, y f la frecuencia de la onda asociada a dicha partícula. Ello obligaba a admitir, para la luz, una naturaleza dual, corpuscular y ondulatoria. También Niels Bohr (1885-1962) construyó su célebre modelo del átomo aunando las ideas clásicas con la cuantización, en una especie de Teoría Cuántica clásica que no prosperó más allá del átomo de hidrógeno. Bohr, defensor de la nueva Física, fue un gran amigo de Einstein, que, como es sabido, fue siempre crítico con la Mecánica Cuántica. Su conocida frase "Dios no juega a los dados con el Universo" exasperaba a Bohr, que llegó a decirle: "¡Albert, deja de decirle a Dios lo que tiene que hacer!".
La teoría cuántico-conservadora de Bohr era insuficiente para explicar los resultados de las experimentaciones. Había que buscar nuevos enfoques y horizontes, había que "penetrar en tierra nueva", en acertada frase de Heisenberg, uno de los padres de la nueva Física.
Actualmente sabemos que debemos mirar la Física con "ojos clásicos" si se trata de objetos o situaciones que nos son cotidianas y próximas, pero que esta mirada debe cambiarse a "relativista" para grandes velocidades y a "cuántica" para dimensiones atómicas.
3.- PENETRANDO EN TIERRA NUEVA
Había estallado la "bomba Plank" en 1900, y las dos "bombas Einstein", la Relatividad, en 1905 y 1916. Pero aún había más.
En 1924, Louis de Broglie (1892-1986) presentó una tesis doctoral audaz. Los electrones, componentes de la materia, deberían comportarse, al igual que los fotones de la luz, como partículas y como ondas, suposición teórica que fue comprobada experimentalmente poco después por Davisson y Germer al lograr la interferencia con electrones. La dualidad onda-corpúsculo se podía ampliar a toda la materia (protones, átomos), siendo la longitud de onda asociada a una partícula material, de momento lineal p = m · v
λ = h/(m · v)
En objetos macroscópicos es indetectable la onda asociada, dado el pequeño valor de h, que resulta menor que el más pequeño error experimental, y en el caso de ondas hertzianas, su momento es indetectable, por lo que en el primer caso hablamos sólo de partículas y en el segundo sólo de ondas. Pero en el caso de partículas minúsculas, tanto la longitud de onda como el momento son detectables, por lo que los aspectos corpuscular y ondulatorio hay que tratarlos conjuntamente.
Siguiendo las ideas de De Broglie, Erwin Schroedinger (1887-1961), desarrolla una teoría matemática de las propiedades atómicas, con una serie de postulados que determinan una ecuación fundamental, la célebre ecuación de Schroedinger, que hoy día se considera tan básica como la ley de Newton.
Simultáneamente, Heisenberg (1901-1976) hizo un estudio de la teoría atómica aplicando matemática de matrices y obteniendo idénticos resultados que su ilustre colega. Ambas formulaciones son dos formas alternativas de la nueva y revolucionaria Mecánica Cuántica, y ambos científicos, junto con Max Plank, los padres de la nueva Teoría. Posteriores desarrollos fueron debidos a Born, Jordan, Dirac, Pauli y otros, muchos de ellos premios Nobel.
La Mecánica clásica se basa en unos principios generales, tales como la conservación de la energía, del momento lineal y del momento angular en sistemas aislados. Estos principios siguen vigentes en la nueva Mecánica, pero se introducen conceptos nuevos que modifican profundamente la concepción del mundo físico: DUALISMO, INDETERMINACION, CUANTIZACION. El primer problema de la Mecánica Cuántica es obtener la función ondulatoria Ÿ para cada partícula o sistema dinámico concreto. Aunque Ÿ se denomine corrientemente función de onda, resulta más propio llamarla amplitud de las ondas estacionarias asociadas a la partícula.
Ya que la intensidad de una onda es proporcional al cuadrado de la amplitud y refiriéndonos a un movimiento unidireccional, es lógico tomar Ÿ2dx como la probabilidad de encontrar la partícula en el intervalo dx alrededor del punto x. En general, la probabilidad por unidad de longitud o densidad de probabilidad es:
d = Ÿ2
4.- LA ECUACION DE SCHRODINGER
La ecuación de Schroedinger representa una parte esencial de la doctrina general de la Física moderna. Toda partícula en movimiento lleva asociada una onda Ÿ, cuya fórmula es:
d2Ÿ/dx2 +(8 p2 m)/h2 (E - V) Ÿ = 0 (1) equivalente a
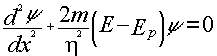 s
s
ecuación válida para casos estacionarios y problemas en una sola dirección, donde E es la energía total de la partícula, V la energía potencial y m la masa de la partícula a la que se asocia Ÿ. La deducción es simple; en Mecánica Cuántica, p = h/f y su correspondiente onda estacionaria,
Ÿ = Aeipx/h
Derivando esta expresión se llega a (1). En el caso de encontrarnos en el espacio, basta con sustituir el primer término de (1) por la suma de las tres derivadas parciales segundas en las tres direcciones del espacio, es decir, por la laplaciana de Ÿ, con lo que se obtendría una ecuación más general (2).
Como se indicó anteriormente, las aplicaciones cuánticas introducidas por Bohr para explicar su modelo de átomo fueron insuficientes, aunque produjera grandes éxitos para el átomo de hidrógeno en las experiencias de la época. Sin embargo, nuevos hechos experimentales determinaron sucesivas ampliaciones de la teoría para poder explicarlos, como las siguientes:
a) Teoría de Sommerfeld: discípulo de Bohr, desarrolló a partir de 1915 una visión más amplia de la teoría: órbitas elípticas, con la introducción de un segundo número cuántico l, desarrollo matemático de la estructura espacial del átomo, consideración de que el electrón en movimiento orbital equivale a una corriente eléctrica con producción de un campo magnético, etc.
b) Efecto Zeeman: existencia de una interacción cuantificada entre el magnetismo del átomo y el campo externo, lo que implica orientaciones orbitales determinadas por un nuevo número cuántico magnético.
c) Spin del electrón: el electrón gira sobre su propio eje a la vez que el movimiento de rotación sobre el núcleo, por lo que tiene momento angular orbital y momento angular propio o spin, con lo que se introduce un cuarto número cuántico. La mejor de las teorías sobre los multipletes, la idea del cuarto número cuántico, se debió a Wolfgrang Pauli, en 1924, en su descripción del spin del electrón. Pauli fue uno de los componentes más importantes del grupo de científicos que crearon la Teoría cuántica, el que formuló en 1925, lo que hoy se conoce como el Principio de Exclusión de Pauli, según el cual dos electrones no pueden tener nunca los cuatro números cuánticos iguales.
d) Modelo vectorial: acoplamiento LS, que origina nuevos niveles energéticos que explicaban los resultados espectroscopios más ajustadamente.
e) Reglas de selección: con todas las modificaciones anteriores se podían predecir más rayas espectrales que las detectadas experimentalmente, por lo que se establecieron unas reglas restrictivas a las variaciones de los números cuánticos.
Toda esta obra científica constituye la denominada Mecánica Cuántica antigua, y es a partir de 1926 cuando se desarrolla la moderna, principalmente por Schroedinger y Heisenberg. La aplicación de la ecuación de Schroedinger al átomo de hidrógeno, un protón nuclear y un electrón cortical, ofrece el modelo actual más satisfactorio y comúnmente aceptado. En la ecuación (2), m es la masa reducida del sistema protón-electrón, y V es el potencial electrostático
V = -e^2/4Πσr
La resolución de esta ecuación se hace expresando la laplaciana en coordenadas polares, r, ceta y fi, y poniendo a la función de onda Ÿ como el producto de tres funciones de dichas coordenadas. Esto permite calcular por separado r, ceta y fi de tres ecuaciones independientes, relacionadas cada una de ellas con un número cuántico. Así aparecen los números cuánticos de la teoría antigua de una manera más natural y también se obtienen los valores cuantizados de la energía que coinciden con los de Bohr.
Lo característico de este método cuántico seguido es que muestra al electrón en torno al protón de otra manera que la descripción clásica (órbita electrónica). Las órbitas de Bohr-Sommerfeld y epígonos son sustituídas por probabilidades de encontrar al electrón a una determinada distancia del núcleo, a partir de Ÿ y de su interpretación cuántica Ÿ^2, que determina los orbitales atómicos. La función de onda Ÿ determina el correspondiente orbital atómico y Ÿ^2 representa la probabilidad de encontrarlo, es decir, la distribución de carga, cuyo cálculo conduce a las conocidas formas geométricas de los orbitales (los esféricos s, los husos p, las formas más complicadas de los d, etc.)
La dualidad onda-partícula explica el átomo. La existencia de órbitas permitidas en el átomo de Bohr fue un misterio cuando fue propuesto el modelo por primera vez. Ahora comprendemos que son las únicas órbitas para las que las descripciones del electrón como onda y partícula son consistentes; cuando la órbita del electrón es estable y su onda encaja, conseguimos una órbita permitida. Así, las órbitas de Bohr son aquellas para las que no constituyen ninguna diferencia si el electrón es una partícula o una onda.
5.- RESOLUCIONES ASEQUIBLES DE LA ECUACION DE SCHROEDINGER
5.-1.- PARTICULA LIBRE
Clásicamente, una partícula libre es la que no está sometida a ninguna fuerza exterior. En estas condiciones, la Mecánica Clásica indica que la partícula debe permanecer en reposo o en movimiento conservando su velocidad (y por tanto, su momento y su energía). También es indudable que, clásicamente, podemos medir la posición x y el momento p con toda precisión. El comportamiento cuántico de la partícula es muy distinto, y de él tendremos conocimiento mediante la aplicación de la ecuación de Schroedinger (1).
Excluyendo un estudio de mayor rigor, se puede admitir la solución:
Ÿ = A sen(ψx +Φ ) (3)
siendo ψ la pulsación y Φ la fase, donde ψ es la raíz cuadrada de 2mE/h. Según la interpretación cuántica, Ÿ^2 dx representa la probabilidad de localización de la partícula en una región del espacio comprendida entre x y x + dx. La gráfica de Ÿ^2 es una sinusoide con sus correspondientes máximos (probabilidad máxima) y mínimos (nula probabilidad).
Si la partícula es microscópica, es decir, m y E grandes en comparación con h, la longitud de onda λ = h/2mE (inversa de ψ) tiende a 0, de suerte que los máximos y mínimos están prácticamente juntos, los saltos son indiscernibles y se obtiene un promedio de Ÿ^2 constante, de acuerdo con la descripción clásica. En caso contrario, el comportamiento de la partícula es cuántico.
5.-2.- PARTICULA CONFINADA
Otro ejemplo de resolución asequible de la ecuación de Schroedinger es una partícula que puede moverse en un recinto unidimensional, comprendido entre x = 0 y x = L. En Física no es difícil encontrar sistemas reales que se aproximen a esta idealización. Para un sistema así, es aplicable la ecuación (1), cuya solución es del tipo
Ÿ = A sen (2mE)1/2/h x
siendo E = n^2 · h^2/8mL^2. Esta expresión indica la cuantización de la energía. Ya que n no puede tomar el valor 0, pues el número cuántico principal sólo puede tomar los valores de los números enteros 1, 2, 3, etc., se excluye la posibilidad clásica E = 0. El valor mínimo de la energía es el proporcionado por n = 1
E1 = h^2/8mL^2
que se denomina energía residual o energía del punto cero. La existencia de esta energía residual choca con la idea clásica de que en el cero absoluto cesa todo movimiento: el comportamiento extraño del helio a bajas temperaturas, no clásico, se explica cuánticamente por la acción de la tal energía residual, y constituye una confirmación experimental de la teoría. Para sistemas microscópicos, al dar valores a n en E1, los valores obtenidos están suficientemente separados. Para una partícula microscópica, los niveles están tan próximos que resultan indistinguibles.
6.- PRINCIPIO DE INDETERMINACION
En la Física clásica, se admite que cualquier variable (posición, velocidad, energía), puede ser especificada y medida con la precisión que queramos; en teoría, con toda precisión, aunque en la práctica haya dificultades para ello por el error cometido debido a los instrumentos usados para la medición. Heisenberg, en 1927, como consecuencia de un análisis penetrante del comportamiento de los sistemas microfísicos, estableció que en estos dominios tal principio clásico de determinación no era válido. Existe un límite para la precisión que constituye el Principio de Indeterminación o Incertidumbre; cuando nos referimos a una expresión específica cuantitativa de este principio, se tiene una relación de indeterminación.
Una primera relación de indeterminación obtenida por Heisenberg, es que la incertidumbre en el momento lineal ∆ p y la incertidumbre en la posición de la partícula ∆ x, verifica
∆ p· ∆ x = h
de modo que su producto es del orden de la constante de Plank h. Es imposible medir la posición y el impulso, al mismo tiempo, con exactitud completa. Heisenberg y otros científicos examinaron toda suerte de procedimientos idealizados para observar simultáneamente estas magnitudes con precisión absoluta, pero ninguno de ellos fue capaz de vulnerar el Principio de Incertidumbre.
En los sistemas microfísicos, la interacción observador-observable debe tener especial relevancia; por ejemplo, si queremos observar un electrón con un visor especial, de alguna manera tendremos que iluminarlo con luz (fotones). Pero los fotones colisionan con el electrón, y éste debe experimentar una modificación en su momento, que es razonable pensar ser del mismo orden que h/œ; cuanto mayor sea la longitud de onda, menor será la indeterminación de p. Por otra parte, la determinación de la posición del electrón presenta una incertidumbre ∆x, que es razonable sea al menos del orden de magnitud de la longitud de onda de la luz utilizada, ∆x = œ. Esta expresión muestra que cuanto menor sea la longitud de onda, menor será la indeterminación de la posición. La relación de indeterminación se obtiene multiplicando las ecuaciones anteriores
∆x ∆p = h
Una segunda relación de indeterminación sería la que implica a la energía y al tiempo en que tiene lugar la emisión o transmisión de dicha energía
E = p^2/2m ∆E = v ∆ p
Como v = ∆ x/∆ t, también ∆t = ∆x/v
Multiplicando estas expresiones se obtiene ∆E ∆t = ∆x ∆p y en definitiva
∆E ∆t = h
Por la pequeñez de h, la relación de indeterminación no tiene relevancia alguna en la Macrofísica, en los fenómenos a escala habitual, pero está siempre presente en los fenómenos a escala atómica o subatómica (Microfísica).
Las sorprendentes conclusiones del Principio de Indeterminación, publicadas en 1927, indujeron a muchos científicos (no a Dirac o a Bohr, por supuesto) a pensar que se afirmaba que sus técnicas no eran lo suficientemente buenas como para medir simultáneamente posición y momento, malentendido que está aún vigente. Cuando Heisenberg afirma al final de su trabajo: "no podemos conocer, por principio, el presente en todos sus detalles", la teoría cuántica se libera del determinismo de las ideas clásicas. Aunque las relaciones de incertidumbre habían sido deducidas a partir de las ecuaciones fundamentales de la Mecánica Cuántica, algunos físicos comenzaron a enseñar la teoría cuántica a partir de las relaciones de incertidumbre, como el mismo Pauli, tendencia que se sigue en la enseñanza actual.
Las relaciones de incertidumbre llevan, entre otras, a la siguiente conclusión: no es posible predecir el futuro, éste es impredecible e incierto; sin embargo, sí se puede saber exactamente la posición y el momento en el pasado, luego éste está perfectamente definido, sabemos de dónde venimos pero no a dónde vamos. Según la "interpretación de Copenhage", dirigida por Bohr, mientras en la Física clásica concebimos que un sistema de partículas funciona como un reloj, independientemente de que sea observado o no, en Física cuántica el observador interactiva con el sistema, en tal medida que el sistema no puede considerarse con una existencia independiente; en este sentido, la Relatividad es una teoría clásica. Hay límites al conocimiento sobre lo que un electrón está haciendo mientras se le observa, pero no se tiene ni idea de lo que está haciendo cuando no le observamos.
7.- CUESTIONES Y PARADOJAS CUANTICAS
7.-1.- EL GATO DE SCHROEDINGER
Es posible montar un experimento de forma que exista una probabilidad exacta del 50% de que uno de los átomos de una muestra de material radiactivo se desintegre en un cierto tiempo y que un detector registre la desintegración, si se produce. Supongamos el experimento confinado en una caja, dentro de la cual hay un gato vivo y un frasco de veneno, preparado todo de tal forma que si ocurre la desintegración radiactiva, el recipiente del veneno se rompe y el gato muere. En el mundo actual existe un 50% de probabilidades de que el gato resulte muerto, y sin mirar dentro de la caja podemos decir que el gato estará vivo o muerto.
Pero en el mundo cuántico, como resultado de la Teoría, ninguna de las dos posibilidades tiene realidad salvo que sea observada: la desintegración atómica ni ha ocurrido ni ha dejado de ocurrir y por lo tanto, el gato ni ha muerto ni ha dejado de morir, en tanto no miremos dentro de la caja para ver lo que ha pasado. Los científicos que aceptan la versión ortodoxa de la Teoría Cuántica, dicen que el gato existe en cierto estado indeterminado, ni vivo ni muerto, hasta que un observador mire dentro de la caja para ver el resultado. N
NADA ES REAL SALVO SI SE OBSERVA.
Para Einstein, la idea era inaceptable: debe existir algún mecanismo subyacente que hace posible la genuina y fundamental realidad de las cosas, pero murió antes de que fuese capaz de encontrar, en algún tipo de experimento, esta realidad subyacente. En el verano de 1982, un equipo de la Universidad de París encabezado por Alain Aspect, completó una serie de experimentos tratando de encontrar esa realidad subyacente del mundo cuántico. A este mecanismo se le ha denominado "variables ocultas", y el experimento se refería al comportamiento de dos fotones viajando en direcciones opuestas desde una misma fuente. Los resultados fueron claros: no existe la realidad subyacente; la palabra realidad no es un concepto utilizable para estudiar el comportamiento de las partículas que integran el Universo. Al mismo tiempo, dichas partículas parecen formar parte de algún todo indivisible y cada una acusa lo que acontece a las restantes.
7.-2.- LA CONTROVERSIA BOHR-EINSTEIN
El gran debate entre Bohr y Einstein sobre la teoría cuántica comenzó en 1927 y continuó hasta la muerte de Einstein en 1955. Einstein trataba de diseñar un experimento en el que sería teóricamente posible medir dos magnitudes físicas complementarias simultáneamente, la posición y el momento de una partícula o su energía exacta en un preciso instante. Bohr y Born trataban de demostrar entonces cómo el experimento imaginado por Einstein no podía llevarse a cabo en la forma requerida para socavar los cimientos de la Teoría Cuántica. Un ejemplo fue el experimento del reloj en la caja, refutado por Bohr. Einstein aceptó la crítica de Bohr de éste y otros experimentos imaginados, y a principios de la década de los 30 presentó una nueva clase de test imaginados de las reglas cuánticas.
Entre 1934 y 1935, Einstein elaboró en Princeton, junto con Boris Podolsky y Nathan Rosen, un artículo en el que se presentaba lo que se conoce como la Paradoja E.P.R. De acuerdo con ella, existe una realidad objetiva, un mundo de partículas con momento y posición definidas simultáneamente de forma precisa, aún cuando no están sometidas a observación. Si tenemos un núcleo que se desintegra en dos partículas idénticas, esas partículas deben aparecer inversas la una de la otra; si giran, una se moverá en el sentido de las agujas del reloj y la otra en sentido contrario. Si dejamos que ambas viajen una larga distancia y luego medimos una de ellas, la otra tiene que estar girando en sentido contrario y en consecuencia, argumentaba Einstein, ambas partículas debían tener esos spins todo el tiempo, fueran medidas o no. Esto demostraba que las partículas cuánticas tenían realmente propiedades definidas todo el tiempo, fueran medidas o no, y que el Principio de Incertidumbre era tan sólo el resultado de nuestra incapacidad de medirlas. Por lo tanto, la auténtica teoría que describe el mundo cuántico no tendría necesidad de explicaciones probabilísticas.
Einstein era una persona honesta, siempre dispuesta a aceptar la evidencia experimental sólida; si hubiera vivido para verlo, ciertamente habría sido persuadido por las recientes confirmaciones experimentales de que estaba equivocado. La realidad objetiva no tiene cabida en una descripción fundamental del Universo.
7.-3.- VIAJE EN EL TIEMPO
El movimiento en el espacio puede ocurrir en cualquier dirección y después en la opuesta. El movimiento en el tiempo sólo tiene lugar en una dirección en el mundo de cada día, y ello parece regir también en el mundo de las partículas. Sin embargo, nuevos desarrollos de modelos cuánticos parecen refutar la idea de una única dirección temporal. De hecho, tanto la Teoría cuántica como la Relatividad permiten el viaje en el tiempo, o más explícitamente, niegan que dicho viaje sea imposible, aunque, eso sí, muy difícil y muy improbable.
7.-4.- ALGO DE NADA
Las cuatro fuerzas fundamentales que dominan la Naturaleza, gravedad, nuclear fuerte, nuclear débil y electromagnética, se entienden hoy como interacciones. Pero, ¿de dónde surgen las partículas portadoras de la interacción? De ningún sitio, según el Principio de Incertidumbre: son algo de nada. En teoría cuántica, pueden perfectamente aparecer partículas de la nada, recombinarse y desaparecer antes de que el Universo en general se aperciba de la anormalidad.
El vacío es en sí mismo un hervidero de partículas virtuales, incluso cuando no hay partículas reales presentes. Y no se trata de una simple consecuencia de las ecuaciones, puesto que sin tener en cuenta el efecto de estas fluctuaciones del vacío, no se obtienen los resultados correctos en los problemas que afectan a las colisiones entre partículas. Las partículas virtuales y las fluctuaciones del vacío son tan reales como el resto de la teoría cuántica; tan reales como la dualidad onda-corpúsculo o el Principio de Incertidumbre.
El axioma fundamental de la Mecánica Cuántica es que ningún fenómeno elemental es un fenómeno hasta que no sea un fenómeno detectado. Todo esto no tiene sentido en el mundo cotidiano, en el mundo microscópico, pero cada cosa del mundo microscópico está constituída por partículas que obedecen las reglas cuánticas; todo lo que se considera real está constituído por elementos que no pueden ser considerados como reales...¿qué otra cosa cabe sino afirmar que todo debe estar basado en la estadísticas de billones de billones (añádanse los ceros que se deseen) de tales actos con participación del observador?
Para Wheeler, el Universo entero es como un circuito autoexcitado y participativo: tras el Big Bang y miles de millones de años, se producen seres capaces de observar el Universo, y los actos de participación del observador producen, a su vez, una realidad tangible al Universo, no sólo al presente, sino a todo el pasado desde el principio. Observar los fotones de la radiación de fondo cósmica, el eco del Big Bang, puede que sea la causa del Big Bang y del mismo Universo.
Todo esto, que puede parecer pura especulación matematico-cuántica, fue sólidamente evidenciado con el experimento de Aspect, a comienzo de la década de los 80, la prueba de que las extrañas peculiaridades cuánticas no son sólo reales, sino también observables y medibles.
7.-5.- LA PRUEBA EXPERIMENTAL
La demostración directa y experimental de la realidad paradójica del mundo cuántico se basa en versiones modernas del experimento imaginado de E.P.R. Los experimentos modernos no manejan las medidas de la posición y del momento de las partículas, sino las del spin y la polarización. La innovación conceptual apareció en 1964 en un artículo de John Bell, físico del CERN; el problema planteado no es sino el que Einstein y sus colegas plantearon en los años 30, pero un experimento práctico vale más que medio siglo de discusión sobre el significado del experimento teórico, y Bell proporcionó a los experimentalistas una forma de medición práctica. El teorema de Bell hace de las argumentaciones sobre la realidad de la Mecánica Cuántica una cuestión experimental. El físico escocés John Bell señaló que, examinando las cantidades que podían ser medidas, como la relación entre la dirección en la que se mueve la partícula y la dirección de su spin, se podía comprobar la idea básica detrás de la paradoja de EPR en el laboratorio.
Hizo esto demostrando que había ciertas relaciones entre esas cantidades que se mantenían si la partícula tenía realmente un spin definido entre el momento en que era emitida y el momento en que era medida, pero que se mantendría un conjunto distinto de relaciones si la partícula tenía que ser descrita por una función ondulatoria durante este período de tránsito (es decir, si como dictaba la Mecánica Cuántica, no tiene un spin definido cuando no está siendo medida).
El test de Bell es un experimento difícil de realizar ya que implica medir spins de muchos pares de protones al azar y rechazar aquellas medidas que se refieren a la misma componente del spin para ambos miembros del par; de los siete primeros tests de Bell realizados, cinco están a favor de la Mecánica Cuántica. Desde mediados de los 70, se han llevado a cabo aún más tests, diseñados para eliminar toda posible objeción al experimento. El test definitivo implica un cambio en la estructura del experimento, en la línea del experimento de Wheeler acerca de la doble rendija.
Este es el experimento con el que el equipo de Alain Aspect, en la Universidad de París, logró en 1982 la última confirmación cuántica; tras la publicación de los resultados obtenidos, nadie duda de la confirmación de las predicciones de la Física cuántica. El equipo de Aspect realizó los tipos de experimentos sugeridos por Bell y hallaron que las predicciones de la Mecánica Cuántica, con sus electrones y fotones probabilistas, tenían razón: un electrón no tiene realmente un spin definido hasta que es medido. Así, parece que la Naturaleza ha decidido simplemente hacer el mundo cuántico distinto al mundo al que estamos acostumbrados.
Debemos enfrentarnos a las cosas a nivel cuántico a través de ecuaciones matemáticas, aunque nunca podamos llegar a verlas o fotografiarlas. Esto resulta duro, incluso para los físicos endurecidos, pero es así.
El experimento de Aspect conduce a un punto de vista del mundo diferente del que establece nuestro sentido común. Las partículas que una vez estuvieron ligadas por una interacción, continúan, en cierto sentido, siendo partes de un único sistema, y responden conjuntamente a interacciones posteriores; los átomos del cuerpo humano están formados por partículas que una vez estuvieron estrechamente ligadas en el Big Bang con partículas que ahora forman parte de alguna estrella lejana y con partículas que constituyen el cuerpo de alguna criatura viviente de algún planeta distante aún por descubrir. Todos somos parte de un sistema único, al igual que lo eran los dos fotones viajeros del experimento de Aspect. Teóricos como d'Espagnat y David Bohn señalan que hay que aceptar que, literalmente, cada cosa está conectada con todo lo demás, y sólo un tratamiento holista del Universo resulta apropiado para explicar fenómenos tales como la consciencia humana.
A principios de 1983, científicos de la Universidad de Sussex, en Inglaterra, anunciaban las conclusiones de experimentos que proporcionan una confirmación independiente de la interconexión de las cosas a nivel cuántico.
8.- OTROS MUNDOS
La interpretación de Copenhague se justifica completamente mediante los experimentos, pero aún así resulta intelectualmente insatisfactoria. ¿Qué ocurre con todos aquellos mundos cuánticos fantasmales que se colapsan con sus funciones de onda cuando se efectúa una medida de un sistema subatómico? ¿Cómo puede una realidad oculta, ni más ni menos real que la que se mide, desaparecer cuando se efectúa la medida?. La mejor respuesta consiste en afirmar que las otras realidades alternativas no desaparecen, y que el gato de Schroedinger ciertamente está tan vivo como muerto al mismo tiempo, pero en dos o más mundos diferentes. La interpretación de Copenhague y sus implicaciones prácticas están totalmente contenidas en una visión más completa de la realidad: la interpretación de la existencia de otros mundos.
Cuando nos referimos a "otros mundos", nos estamos refiriendo a otros Universos. Y dentro de este concepto, hay que resaltar dos formas de interpretarlos. La primera interpretación serían los mundos paralelos, como infinitas ramas de un árbol que parte del Big Bang. Cada suceso deriva cada una de las ramas, con lo cual nos encontramos un número ilimitado de mundos, cada uno surgido de una elección.
La segunda interpretación de los otros mundos consiste en la suposición de infinitos Big Bangs, cada uno de los cuales originario de un Universo, siendo producidos cada uno de los Big Bangs por una fluctuación del vacío cuántico, donde la aparición de partículas y su desaparición completa un ciclo Big Bang-Big Crunch extremadamente largo. Por otra parte, suponiendo un Universo oscilante, cíclico, se puede considerar otro Universo al siguiente originado por el Big Bang que sigue al Big Crunch de uno dado. Interpretando que los sucesivos ciclos de un Universo oscilante pertenecen al mismo Universo, serían las anteriores dos interpretaciones las utilizadas para referirse a "otros mundos".
Una de las consecuencias que se derivan de las ecuaciones de la Mecánica Cuántica es la existencia de otros mundos, posiblemente un número infinito de ellos, separados en el tiempo de nuestra realidad, paralelos a nuestro propio Universo pero eternamente desconectados de él. Esta interpretación de la existencia de otros mundos a partir de la teoría cuántica tuvo su origen en el trabajo de Hugh Everett, un licenciado por la Universidad de Princeton en la década de los 50, en una tesis doctoral animada por John Wheeler. La interpretación de Everett consiste en admitir que las funciones de onda superpuestas del Universo entero, las realidades alternativas que interaccionan en el nivel cuántico, no se colapsan. Todas ellas son igualmente reales y existen en una parte concreta del espacio y del tiempo.
Cuando se efectúa una medida en el nivel cuántico, es forzoso, en virtud del proceso de observación, seleccionar una de esas alternativas, que se convierte en lo que se conoce como mundo real. Esto es más sencillo de comprender en la paradójica caja donde sestea el gato de Schroedinger. Las ecuaciones de la Mecánica Cuántica indican que en el interior de la caja del famoso experimento, hay aspectos de una función de onda de un gato vivo y de un gato muerto.
La interpretación convencional de Copenhague considera que ambas funciones de onda son igualmente irreales, y sólo una de ellas es una realidad cuando se observa dentro de la caja. La interpretación de Everett acepta las ecuaciones cuánticas en sentido literal y afirma que ambos gatos son reales; hay un gato vivo y hay un gato muerto, pero están localizados en mundos diferentes. El Universo se desdobla en dos versiones de sí mismo, y aunque suena a ciencia-ficción, el asunto es mucho más profundo y se basa en unas ecuaciones matemáticas inobjetables, de acuerdo a la premisa de aceptar literalmente el formalismo cuántico.
A pesar de su perfecto tratamiento matemático, la nueva interpretación de Everett de la Mecánica Cuántica apenas causó impacto entre la comunidad científica en 1957, quizá por apartarse de la interpretación deCopenhague que nunca ha fallado en cuestiones de tipo práctico. Tuvieron que transcurrir diez años para que Bryce DeWitt, de la Universidad de Carolina del Norte, volviese sobre la idea de Everett, considerando incluso hasta dónde podía llegar el desdoblamiento constante de mundos. Podría hablarse de una superautopista con millones de carriles paralelos, y aunque el tema ha sido tratado en la ciencia-ficción especulando con la posibilidad de cambiar de carril, pasándonos al mundo de al lado, las matemáticas no son compatibles con tan sugestiva imagen.
Un viaje en el tiempo, en nuestro propio mundo, siempre ha sido negado por las teorías convencionales, por las paradojas que implican, como la de volver atrás en el tiempo y matar al propio abuelo antes de que el padre de uno mismo fuera concebido. A nivel cuántico, las partículas parecen estar involucradas constantemente en tal viaje temporal, y Frank Tipler ha demostrado que las ecuaciones de la Relatividad General lo permiten. Es posible concebir una clase especial de viaje adelante y hacia atrás en el tiempo que no dé lugar a paradojas, y la forma de tal viaje se basa en la realidad de los Universos alternativos.
Volvamos a la paradoja del abuelo: si se vuelve hacia atrás en el tiempo y se mata al abuelo, se está creando, o entrando, en un mundo alternativo, ramificado perpendicularmente al original. En esta nueva realidad, ni el padre ni uno mismo habrían nacido nunca, y no hay paradoja porque uno sigue aún vivo en la realidad original, y lo único que ha hecho es viajar hacia atrás en el tiempo hasta una realidad alternativa. Volviendo atrás y deshaciendo el proceso, esa persona se reintegra en la ramificación original de realidad.
De acuerdo a la interpretación de la teoría de los otros mundos, el futuro no está determinado, pero el pasado sí lo está. Hay muchas rutas para el futuro, y alguna versión de nosotros seguirá por alguna de ellas. Cada una de estas versiones de nosotros mismos creerá que avanza a través del único camino, y se mirará en un único pasado, pero resulta absolutamente imposible conocer el futuro porque hay infinidad de ellos.
La pregunta más importante que falta por contestar dentro de este esquema es por qué nuestra percepción de la realidad habría de ser la que es; ¿por qué la elección de caminos a través del laberinto cuántico que se origina en el Big Bang y llega hasta nosotros, debe conducir precisamente a la aparición de la inteligencia en el Universo?
La respuesta se apoya en el Principio Antrópico. Este postula que las condiciones que existen en nuestro Universo son las únicas condiciones, salvo pequeñas variaciones, que habrían permitido la evolución hasta una vida como la humana. Si el Universo no fuera como es, nosotros no estaríamos aquí para observarlo. El problema sería por qué apareció un mundo ideal para la vida a partir del Big Bang.
El Principio Antrópico afirma que pueden existir muchos posibles mundos y que nosotros somos un producto inevitable de nuestra clase de Universo. Pero, ¿dónde están los otros mundos? ¿Son fantasmas, como los mundos que interaccionan en la interpretación de Copenhague? ¿Corresponden a diferentes ciclos vitales de nuestro Universo, supuesto oscilante? ¿O podrían ser los otros mundos de Everett, todos ellos perpendiculares al nuestro? Esta última es, sin duda, la mejor explicación de que se dispone actualmente.
La mayoría de las realidades cuánticas alternativas no son apropiadas para la vida. Las condiciones necesarias para la vida son muy especiales, y no ha sido el azar el que ha seleccionado estas condiciones, sino la elección. Todos los mundos son igualmente reales, pero sólo aquellos mundos apropiados contienen observadores. El éxito de los experimentos del equipo de Aspect al someter a test la idea de Bell ha eliminado todas, excepto dos, de las posibles interpretaciones que en el curso del tiempo se han presentado en torno a la Mecánica Cuántica: o se acepta la interpretación de Copenhague con sus realidades fantasmales y sus gatos vivo-muertos, o se acepta la interpretación de Everett con sus otros mundos.
Es concebible, por supuesto, que ninguna de las dos posibilidades sea la buena, que ambas alternativas sean erróneas y que aparezca otra interpretación de la realidad cuántica que resuelva todos los problemas, que satisfaga las interpretaciones de Copenhague y de Everet y el test de Bell y que vaya más lejos del conocimiento actual; sin embargo, tras más de medio siglo de intensos esfuerzos dedicados al problema de la realidad cuántica por los mejores cerebros del siglo XX, hay que aceptar que la Ciencia sólo puede ofrecer actualmente estas dos explicaciones alternativas de la forma en que el mundo está construído. Max Jammer, uno de los filósofos cuánticos más relevantes, ha dicho que "la teoría de los otros mundos de Everett es una de las más osadas y la más ambiciosa de las teorías construídas en la historia de la Ciencia". Prácticamente lo explica todo: por ello es la que más atrae. Todo en ella es posible y según las acciones realizadas, se escoge el camino a través de los muchos mundos del cuanto. En nuestro Universo, lo que vemos es lo que hay, no existen variables ocultas, Dios no juega a los dados y todo es real.
Una de las anécdotas que se cuentan sobre Bohr es que cuando, en los años 20, alguien acudía a él con una idea aberrante pretendiendo resolver alguno de los problemas de la Teoría Cuántica, él replicaba: "su teoría es disparatada, pero no lo suficientemente disparatada como para ser verdad". La teoría de Everett es lo suficientemente disparatada como para ser verdadera.
9.- LA HISTORIA CONTINUA
La historia del cuanto aún no se ha terminado, ni mucho menos; existen indicios sobre posibles desarrollos futuros. Así, la QED, la Electrodinámica Cuántica, teoría que explica la interacción electromagnética en términos cuánticos, y que ya floreció en la década de los 40, se ha mostrado tan potente que ha sido usada como modelo para una teoría de la interacción nuclear; teoría que a su vez ha dado origen a la QCD, Cromodinámica Cuántica, llamada así porque involucra la interacción entre los quarks.
Sin embargo, los problemas son muchos. Partiendo de la ecuación de Schroedinger, la pieza clave de la teoría cuántica, el tratamiento matemático correcto del electrón conduce a una masa infinita, energía infinita y carga infinita. Los teóricos eliminan los infinitos de las ecuaciones dividiendo un infinito por otro infinito, y como matemáticamente este cociente es indeterminado, afirman que es precisamente la solución buscada, la masa medida para el electrón. Esta teoría recibe el nombre de Renormalización, y los resultados, al aplicarla, son perfectos, por lo que la mayoría de los teóricos aceptan a la QED como una buena teoría y no se preocupan por los infinitos. A este respecto, Dirac afirmaba en una conferencia en Nueva Zelanda en 1975:
"Estoy altamente insatisfecho de que se considere una buena teoría a aquella que implica despreciar arbitrariamente los infinitos de sus ecuaciones; esto no es razonable matemáticamente".
Deben surgir nuevas teorías cuánticas, y existen interesantes desarrollos que han aparecido dentro de la Física actual y que pueden llegar a satisfacer incluso los requerimientos exigidos por Dirac para constituir una buena teoría.
La Mecánica Cuántica dice muchas cosas acerca de las partículas materiales, pero no dice prácticamente nada sobre el espacio vacío. La proporción entre materia y espacio vacío es mínima: el 99,999% del Universo es espacio vacío, y la teoría cuántica parece indicar que ese espacio vacío hierve de actividad con su enjambre de partículas virtuales. Roger Penrose ha tratado de encontrar una descripción geométrica del vacío y de las partículas del mismo, geometría que implica un espacio-tiempo distorsionado y retorcimientos locales en el espacio-tiempo que se perciben como partículas; puede tratarse de una teoría errónea o imprecisa, pero ataca de frente un gran problema.
Combinando las tres constantes fundamentales de la Física, G, h y c, es posible obtener otra constante, unidad básica de longitud, o cuanto de longitud, que se interpreta como la región más pequeña del espacio que es susceptible de ser descrita con pleno sentido (10^-35 m, longitud de Plank). Del mismo modo, combinando las constantes de forma diferente, se obtiene una y solo una unidad fundamental de tiempo (10^- 43 s, tiempo de Plank). Carece de sentido hablar de longitudes o tiempos inferiores a estos números. Las fluctuaciones cuánticas son despreciables a escala atómica e incluso a nivel de partículas elementales, pero al nivel de Plank el espacio puede entenderse como una espuma de fluctuaciones cuánticas; la idea, de John Wheeler, indica que a nivel cuántico, el espacio-tiempo se hace terriblemente complejo; el espacio vacío podría estar constituído por agujeros negros, del tamaño de la longitud de Plank, estrechamente unidos.
La simetría es un concepto esencial en Física. Las ecuaciones fundamentales presentan simetría temporal; otras simetrías se pueden entender en términos geométricos. Pero hay otras simetrías mucho más difíciles de explicar y que requieren un complejo lenguaje matemático, como la conocida "simetría de gauge"; el Electromagnetismo de Maxwell es una teoría con simetría de gauge, y la QED también. ¿Cómo puede romperse una simetría matemática? Un buen ejemplo se encuentra en el magnetismo, donde la rotura de simetría aparece, por ejemplo, cuando una barra de material magnético se enfría por debajo de una cierta temperatura.
A finales de los años 60, Abdus Salam, en Londres, y Steven Weinberg, en Harvard, elaboraron independientemente un modelo para la interacción débil desarrollado a partir de la simetría matemática ideada por Sheldon Glashow. La interacción electromagnética y la débil se combinan en una simetría, la interacción electrodébil, con bosones mediadores de masa cero. Esta interacción opera sólo bajo condiciones de muy alta densidad de energía, como las del Big Bang, y a energía más baja se rompe espontáneamente, provocando que las interacciones electromagnética y débil sigan caminos distintos.
La importancia de esta nueva teoría es tal que sus creadores obtuvieron el Nobel en 1979, y en 1983, experimentos realizados en el CERN, en Ginebra, con partículas de muy alta energía, confirmaron las predicciones de la teoría. Lo siguiente es pensar: si dos interacciones se pueden combinar en una teoría, ¿por qué no pensar en una gran teoría unificada que englobe a todas las interacciones fundamentales?. El sueño de Einstein está más cerca de verse realizado.
El problema con las teorías gauge, aparte de sus dificultades de renormalización, es que no son únicas. Los físicos buscan una teoría ideal única que requiera sólo cierto número de clases de partículas para explicar el mundo físico, como la Supersimetría, idea surgida en 1974 con los trabajos de Julius Wess, de la Universidad de Karlsruhe y Bruno Zumino, de la Universidad de California. Si se desarrollan las matemáticas apropiadas, se encuentra que existen modos de describir supersimetrías que existieron durante el Big Bang, pero que a continuación se rompieron formando partículas ordinarias en nuestra Física y superpartículas homólogas de grandes masas que existieron durante un pequeño intervalo de tiempo para transformarse en un chorro de partículas de mucha menor masa.
Existen diferentes clases de teorías de campos supersimétricos y numerosas variaciones sobre el mismo tema; en supersimetrías es esencial tener en cuenta la renormalización. En algunas de estas teorías los infinitos se cancelan automáticamente, no en virtud de un procedimiento arbitrario, al aplicar los métodos matemáticos correspondientes.
La Supersimetría no es aún la respuesta final, ninguna teoría supersimétrica explica por sí sola el mundo real. No obstante, hay una teoría supersimétrica particular que merece especial atención, la Supergravedad. Esta teoría se apoya en una partícula hipotética, el gravitón, portadora del campo gravitatorio. Junto a ella hay 8 partículas llamadas gravitinos, 56 reales como quarks y electrones y 98 que son mediadores de interacciones (fotones, bosones, gluones). Aunque los problemas de la Supergravedad son inmensos, es una teoría consistente, finita y no necesita de renormalización.
Todo esto nos lleva al campo de la Cosmología: quizás esta ciencia sea realmente una rama de la Física de partículas. Una idea actual es que el Universo y todo lo que hay en él no es, ni más ni menos, que una fluctuación del vacío que permite la explosión de grandes cantidades de partículas a partir de la nada, que tienen un tiempo determinado y que son reabsorbidas en el vacío.
Un Universo que nace con una bola de fuego del Big Bang, se expansiona durante un tiempo para contraerse después en otra bola de fuego y desaparecer, es una fluctuación del vacío pero a una enorme escala. Esta idea original se remonta al siglo XIX con Ludwig Boltzmann, que especulaba sobre la base de un Universo en equilibrio termodinámico. Edward Tryon, de la Universidad de Nueva York, publicó un artículo en Nature desarrollando la idea del Big Bang como una fluctuación del vacío; si el Universo tiene energía total cero, aplicando el Principio de Incertidumbre (incertidumbre de energía por incertidumbre de tiempo igual a h), el tiempo que puede existir el Universo es verdaderamente muy grande. En una nueva versión de esta teoría, los cálculos proporcionaron que cualquier nuevo Universo cuántico formado como una fluctuación del vacío, debía ser diminuto, y un fenómeno de vida tan corto que ocuparía solo un pequeño volumen en el espacio-tiempo. Pero entonces los cosmólogos descubrieron una forma de hacer que este minúsculo Universo se desarrollara a través de una drástica expansión que podría hacerlo crecer hasta el tamaño del Universo en que vivimos: es la teoría de la Inflación.
La idea original es de Alan Guth, del Instituto de Tecnología de Massachusetts. Parte de la imagen de un Universo primitivo muy caliente y muy denso, con una edad de 10^-35 s y temperatura de 10^28 K, en el que todas las interacciones, excepto la gravedad (la teoría todavía no la incluye), estaban unidas en una interacción simétrica. Al enfriarse el Universo, la simetría se rompió, y las fuerzas fundamentales siguieron su camino separadamente. Por lo tanto, los dos estados del Universo, el anterior y el posterior a la rotura de la simetría, son muy diferentes entre sí. La expansión producida por la rotura de la simetría habría sido exponencial, doblándose el tamaño del Universo cada 10^-35 s; en menos de un segundo, esta explosión habría inflado una región del tamaño de un protón hasta las dimensiones del Universo observable. La versión de Guth del Universo inflacionista no intenta explicar de dónde viene la burbuja inicial, pero puede equipararse fácilmente con una fluctuación del vacío del tipo descrito por Tryon.
La unificación de la Teoría Cuántica y la Gravedad es posible, aun cuando no existan conclusiones definitivas aún, y puede ser que tarden mucho tiempo en enunciarse...pero la Física es en gran parte exploración de lo desconocido. Si la Física deja de estudiarse alguna vez, el mundo sería un lugar mucho menos interesante para vivir.
© 2020 Javier de Lucas Linares