ECUACIONES CUANTICAS
La expresión de la ecuación de Schrödinger de amplitud
(1)
permite predecir a nivel cuántico la probabilidad de encontrar una partícula simple, en este caso el electrón, para cada posición que pueda ocupar en el espacio. Así, si la Física clásica establece zonas prohibidas que de ninguna manera el electrón puede ocupar, la ecuación de Schroedinger establece que hay cierta probabilidad, si bien pequeña, de encontrar el electrón en zonas prohibidas por la Física clásica, como ha sido comprobado experimentalmente.
En el caso del oscilador armónico, la Física clásica establece
la imposibilidad de que el electrón se encuentre más allá de la elongación 
, sin embargo la
ecuación de Schroedinger para este caso establece que hay una pequeña
probabilidad de encontrarlo más allá de 
.
Ecuación de Onda Electromagnética
La teoría electromagnética establece la ecuación de una onda. Si H es la intensidad del campo magnético de la onda y sólo consideramos el desplazamiento según el eje X tenemos:
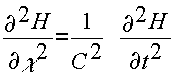(2)
La solución de la ecuación (2) es:
(3)
donde
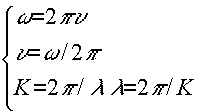
Para una magnitud de la onda cualquiera, en forma genérica la llamamos y
(4)
Onda de Debroglie
Einsten estableció la ecuación de energía producida por la masa (m) transformada en energía.
(5)
E corresponde a la energía total. En el caso de un fotón o partícula cualquiera (por ejemplo el electrón) en movimiento y completamente libre, E será igual a la energía cinética únicamente. Pero si la partícula esta confinada, E será igual a la energía cinética más la energía potencial E = T + Ep.
Debroglie establece la ecuación de la cantidad de movimiento no sólo para el fotón, sino también para cualquier partícula, por ejemplo el electrón.
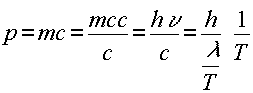(6)
donde m es la masa del electrón y c es la velocidad de la luz
(7)
donde la h es la constante de Plank
® 
(8)
® 
(9)
reemplazando k y w de las ecuaciones (8) y (9) en la ecuación (4) tenemos
(10)
Reemplazamos y por Y porque la ecuación (10) se refiere a la onda partícula, e y corresponde a la de amplitud instantánea de la onda, pero por ser compleja no tiene por el momento interpretación física :
(11)
ECUACION DE SCHRODINGER DEPENDIENTE DEL TIEMPO
La ecuación de Schroedinger dependiente del tiempo, ecuación diferencial que gobierna el movimiento de un electrón es:
(12)
donde Y es una función del desplazamiento x y del tiempo t
Reemplazando en ecuación (12) y separando variables
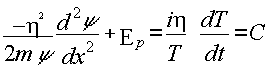(13)
La ecuación de la derecha de (13) es solo función del tiempo
(14)
La solución de la ecuación (14) es:
(15)
La ecuación (11) tiene dos productos, uno dependiente de x y otro dependiente del tiempo. El factor dependiente del tiempo es:
(16)
igualando ecuación (15) con ecuación (16) se llega a la conclusión de que
La parte izquierda de la ecuación (13) en que se ha reemplazado C por E es:
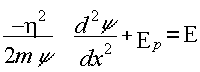(17)
operando
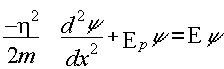(18)
Lo que lleva, despejando, a la Ecuación de Schrodinger de amplitud:
(19)
A la solución Y de esta ecuación se le llama función onda.
Oscilador Armónico
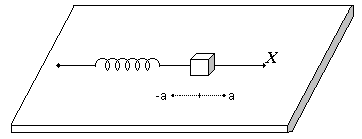
En un resorte, según la ley de Hook, la fuerza de reacción del resorte es proporcional a la elongación:
(20)
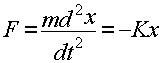De acuerdo a
la primera ley de Newton en un movimiento acelerado
Operando
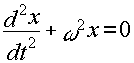(22)
la solución de la ecuación diferencial (22) es:
(23)
que es la solución del oscilador clásico
Oscilador Cuántico
En un resorte la energía potencial es:
(24)
sustituyendo en la ecuación (19) el valor de Ep dado en la ecuación (24)
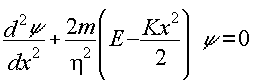(25)
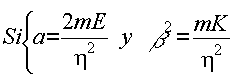
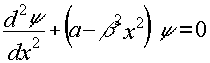(26)
la solución de la ecuación (26) es:
(27)
La solución más general de la ecuación (26) es
(28)
donde f(x) es la solución de
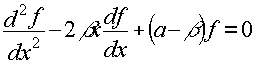que es la
ecuación de Legendre (29)
Esta ecuación diferencial se ha obtenido al introducir la ecuación (28) en la ecuación diferencial de Legendre y tiene infinitas soluciones. Las soluciones son series de potencias con n términos; cuando n = 0 la solución es solo una constante
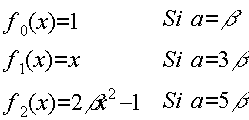
Si a =(2x10+1)b = 21b
Para 
(30)
Que es el mínimo valor de energía que tiene el oscilador
para 
la energía ha aumentado en un escalón igual a hn
para 
la
energía ha aumentado en hn
para a = 2n+1 
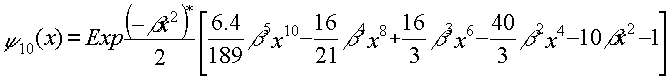
El máximo recorrido del oscilador según el eje x es x = a; en ese instante la energía es solamente potencial e igual a:
(32)
La probabilidad dp de encontrar la masa m en un pequeño intervalo dx localizada a una distancia x del origen es:
ya que en el oscilador clásico x = a cos wt tenemos
(34)
El diferencial de probabilidad es proporcional a
(35)
Hay una
cercana semejanza entre la curva de probabilidad de la clásica masa vibrante y
la curva promedio de y. Es
razonable postular que 
es la probabilidad por unidad de longitud de encontrar un oscilador de
energía 
en una
pequeña longitud dx localizada en x. Esta cantidad es también llamada
densidad de probabilidad. Hay una pequeña probabilidad
de encontrar la partícula en lugares que no son accesibles a la física clásica,
o sea, más allá de 
.
© 2003 Javier de Lucas