Entre los años 1925 y 1930 fue la época de los triunfales logros de la era heroica de la física teórica. Durante esos años se formuló la teoría cuántica, poniendo orden en las aparentemente paradójicas propiedades de los átomos, los electrones y la radiación. Todos los científicos, tanto cosmólogos como biólogos, seguramente estarán de acuerdo en que la mecánica cuántica supera cualquier otro avance conceptual por la amplitud de sus implicaciones científicas, y por las derivaciones «antiintuitivas» que aporta a nuestra visión de la naturaleza; el microcosmos es definitivamente tan extraño como el cosmos. Pero la teoría cuántica no es la obra de ningún «Einstein», sino la de un brillante grupo de investigadores, siendo uno de los más destacados el físico austríaco Erwin Schrödinger.

En 1924, un teórico francés, Louis de Broglie, sugirió que los electrones dentro de los átomos podían ser descritos no sólo como partículas, como lo había planteado Niels Bohr algunos años antes, sino también como ondas. Schrödinger, dos años después, elaboró ese concepto y le dio el andamiaje matemático al descubrir la ecuación que lleva su nombre. Argumentó que los electrones no eran objetos que orbitaran el núcleo, sino que más bien, de alguna forma, se transformaban en ondas. Eliminando el electrón como partícula, Schrödinger afirmó que los cambios en la emisión de energía eran causados no por los saltos orbitales de los electrones, como había dicho Bohr, sino por cambios de un tipo de esquema y frecuencia de onda a otro. Muchos físicos abrazaron esta teoría de la mecánica ondulatoria, puesto que era considerablemente más fácil de visualizar. También implicaba unas matemáticas mucho menos complicadas que las requeridas por el enfoque de la matriz de Werner Heisenberg. .

Con el advenimiento de la mecánica cuántica en 1927, se articularon la hipótesis de Louis de Broglie y el principio de indeterminación de Heisenberg. Ahora, para aplicar el carácter ondulatorio del electrón, se define una función de ondas, Y, utilizando la ecuación de ondas de Schrödinger, que matemáticamente es una ecuación diferencial de segundo grado, es decir, una ecuación en la cual intervienen derivadas segundas de la función Y :

Al resolver la ecuación diferencial, se obtiene la función Y. Esta función depende de una serie de parámetros, que se corresponden con los números cuánticos, tal y como se define en el modelo atómico de Böhr. La ecuación sólo se plasmará cuando esos parámetros tomen determinados valores permitidos (los mismos valores que se indicaron para el modelo de Böhr).

Por otro lado, el cuadrado de la función de onda, Y², corresponde a la probabilidad de encontrar al electrón en una región determinada, con lo cual se está introduciendo en el modelo el principio de incertidumbre de Heisenberg. Por ello, en este modelo aparece el concepto de «orbital»: región del espacio en la que hay una máxima probabilidad de encontrar al electrón.

Ahora bien, si Y es una función exacta de onda molecular que depende de las posiciones de todos los n electrones

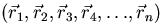
y de las posiciones de todos los N núcleos

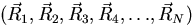
y de las cordenadas de los espines

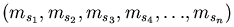
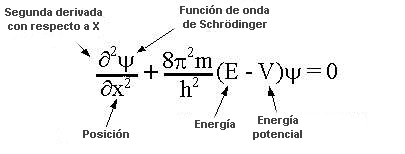
de de los n electrones individuales, la ecuación de Schrödinguer independiente del tiempo puede ser expresada como sigue:

[01]

o, desarrollando los parámetros vectoriales y así los parámetros escalares en la expresión [01], en que adquiere la siguiente forma:

[02]

estando los vectores a los núcleos y los vectores a los electrones definidos como se observa en la figura N° 01. Observamos como en nuestras descripciones separamos las variables dependientes de los núcleos de las dependientes de los electrones mediante un punto y una coma.

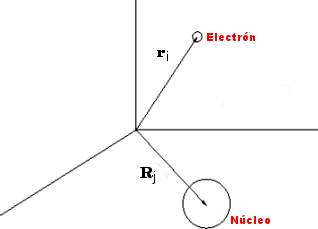
Fig.- N°01

Podemos derivar la forma del hamiltoniano molecular de la fórmula de la energía clásica por la sustitución del momento clásico y de las coordenadas por sus correspondientes operadores. El hamiltoniano total puede ser expresado como sigue:

[03]

o bien, desarrollando la expresión 03, con el objeto de describir el hamiltoniano total de la siguiente manera:

[04]

La ecuación [04] está expresada en unidades atómicas, en que a denota la masa del núcleo M_a y Z_a su carga [05]; ambos parámetros también en unidades atómicas. También se puede reescribir la expresión en el sistema MKS, de la siguiente forma:

[05]

donde q_a corresponde a la carga de un nucleo.

El operador laplaciano D viene formulado por la expresión:

[06]

en que desarrollando la expresión [06] para todos los núcleos , tenemos:

[07]

y, de la misma manera, la expresión [06] para todo electrón es:

[08]

Por otro lado, el hamiltoniano de la expresión [04] puede ser reescrito en la siguiente manera:

[09]

en que el hamiltoniano molecular total es la suma del operador de energía cinética nuclear

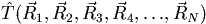
con el operador de energía cinética electrónica

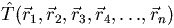
y la representación de los operadores de potencial de interacción electrostática , donde es el operador de potencial de interacción electrostática entre núcleos para todo par núcleo-núcleo -función de los vectores- donde es el operador del potencial de la interacción electrostática entre electrones para todo par electrón-electrón -función de los vectores- y el operador de potencial de interacción electrostática híbrido entre cada núcleo y cada electrón -función de los vectores

-.

Hasta ahora hemos visto cómo se opera con la ecuación de Schrödinger hasta llegar a [02], y hemos desarrollado un hamiltoniano hasta la formulación [09]. O sea, hemos descrito matemáticamente a una partícula inserta en un problema de un átomo. Pero el tema es más complejo. En efecto, en la mecánica cuántica toda la información acerca de una partícula está incluida en su función de onda Y, bien en el espacio de coordenadas, bien en el espacio de momentos. Pero ¿qué pasa con su evolución en el tiempo? Como en la física clásica, se supone que si se conoce toda la información necesaria sobre la partícula en un instante inicial, se puede determinar su comportamiento en el futuro: el principio de determinación. Esto significa en mecánica cuántica que, al dar la función de onda en el instante inicial, podemos calcularla en cualquier otro instante.

 

Se trata de un proceso que se realiza a través de la ecuación de Schrödinger de onda para Y(t), análoga a las ecuaciones de onda clásicas. Esta ecuación sustituye a la ley de Newton para la partícula cuántica. Ahora bien, las diferencias esenciales que se dan entre la ecuación para Y(t)) y las ecuaciones de onda clásica son manifiestas: la ecuación para Y debe contener sólo el primer orden en la derivada temporal para que al dar sólo Y(t = t₀) se pueda determinar su comportamiento en el futuro. En cambio, las ecuaciones clásicas contienen derivadas segundas y por lo tanto requieren dar no sólo la función en el instante inicial sino también su primera derivada temporal.

 

Una partícula libre en la mecánica cuántica tiene como función de onda un paquete de ondas planas cuya dependencia del tiempo ya está determinada. Por eso no es difícil establecer la ecuación que gobierna la evolución en el tiempo en este caso. Si derivamos respecto al tiempo de:

encontramos:

[10]

Por otro lado, tomando el cuadrado del gradiente ² = D (operador de Laplace) tenemos:

[11]

Ahora tomemos la siguiente relación entre w y k:

 

comparando [10] con [11], vemos que se cumple:

[12]

En la segunda igualdad hemos considerado en el espacio de coordenadas que el momento es el operador de gradiente: p = -i. La relación [12] es válida para una amplitud cualquiera Y(k) y, por tanto, para una función de onda cualquiera de una partícula libre, y es precisamente la ecuación de Schrödinger para una partícula libre.

Una de las dificultades que se pueden encontrar en este desarrollo es cómo generalizar [12] cuando las partículas no son libres. Supongamos el caso más sencillo de una interacción dada por un potencial U, donde el operador que actúa sobre Y en el tramo derecho de [12] corresponde a la energía cinética T (p) de la partícula en función de su momento. En el caso libre considerado, coincide con la energía total. En la mecánica clásica la energía total de la partícula expresada como función de su momento y coordenada se llama función de Hamilton H ( r, p ). Para una partícula libre H ( r, p ) = T (p), así que para ella la ecuación [12] puede ser reeexpresada de la siguiente forma:

[13]

donde se considera a H como un supuesto del operador correspondiente a la función hamiltoniana con p como operador de gradiente. Schrödinger postuló que si la partícula está en un campo de fuerzas conservativas dadas por una energía potencial expresada (clásicamente) por U(r), la ecuación para la función de onda conserva su forma [13] con H dada como suma de las energías cinética y potencial

[14]

donde p y r son ahora los operadores de gradiente y de multiplicación, respectivamente. El operador H que resulta se llama hamiltoniano de la partícula. Su sentido físico es el de la energía total. Sus autofunciones, por tanto, son los estados con energía total dada por los autovalores correspondientes de H. Al pasar al espacio de momentos obtenemos la ecuación de Schrödinger para la función de onda f ( t, k ) :

[15]

con H dado por la misma fórmula [14], donde ahora r es el operador de gradiente y p de multiplicación. Señalemos, no obstante, que la energía potencial U (r) puede ser una función bastante complicada. Por ello, el uso de la forma [14] para el espacio ordinario es muchísimo más recomendable.

Ambas formas [13] y [15] pueden recogerse en la ecuación de Schrödinger para el vector de onda Y ( t )

[16]

donde el espacio puede ser cualquiera y la forma de operadores r y p se escoge según el espacio.

La ecuación de Schrödinger no se deduce en la mecánica cuántica, sino que representa un resultado derivado de observaciones empíricas. Sin embargo, se puede justificar a posteriori considerando sus consecuencias y comparándolas con lo que en realidad ocurre en la naturaleza. Con su aplicación se muestra a las ondas como una de las características de la materia y es considerada como uno de los grandes logros obtenidos en el siglo XX. Se trata de una herramienta matemática de gran alcance que se utiliza en la física y en una parte importante de los estudios que se efectúan en química que se ocupan de los problemas de la estructura atómica de la materia.

 

                                                                   © 1987 Javier de Lucas