SINGULARIDAD

Cuando en Física nos estamos refiriendo a la «singularidad» de una masa, estamos pensando en un objeto que --independientemente de su tamaño-- se ha comprimido a tal extremo, que acaba poseyendo una fuerza de gravedad de una magnitud tal que ni siquiera la luz puede escapar del mismo. De acuerdo con la relatividad general, cabe la posibilidad de que una masa reduzca sin límites su tamaño y se autoconfine en un espacio infinitamente pequeño.

 Las singularidades ocurren en el Big Bang, en los agujeros negros y en el Big Crunch (que podría ser considerado como una unión de agujeros negros). Pero para nuestros intereses aquí, nos vamos a referir con un poco de mayor atención a los aspectos de ellas que se encuentran involucrados en los agujeros negros y, tan solo, en forma muy sintetizada, describiremos algunos de los rasgos por los cuales son distinguidas las hipótesis sobre la «singularidad desnuda», la «censura cósmica», etc.

En consecuencia, cuando nos estamos refiriendo a una «singularidad», estamos pensando en una masa con volumen nulo rodeada de una frontera gravitacional llamada «horizonte de sucesos», de la cual nada puede escapar. Para que exista un agujero negro, en alguna parte debe haber una singularidad y, para que ello ocurra, debe estar delimitada en su exterior por un horizonte de sucesos, lo que implica en esencia que no se puede observar desde el exterior la singularidad misma. Específicamente, significa que hay alguna región incapaz de enviar señales al infinito exterior. La frontera de esa región es la que hemos llamado como horizonte de sucesos.

Un mes después de la publicación de la teoría general de la relatividad de Einstein, el físico alemán Karl Schwarzschild descubrió que las ecuaciones conducían a una asombrosa predicción: una región del espacio puede distorsionarse de tal manera que puede quedar aislada del universo exterior. Los objetos pueden entrar en esa región, pero no pueden salir. Hoy llamamos a esa región agujeros negros. Einstein se negó a creer en los agujeros negros, pero en ello estaba equivocado. A primera vista, los agujeros negros de Schwarzschild parecen ser los predichos en la teoría de Newton. Pero solamente la teoría de Einstein puede explicar correctamente cómo se comportan el espacio, la luz y la materia en las proximidades de un agujero negro. Los matemáticos han utilizado la teoría general de la relatividad para calcular lo que sucede en el interior de un agujero negro.

De acuerdo con la relatividad general, cabe la posibilidad de que una masa reduzca sin límite su tamaño y se autoconfine en un espacio infinitamente pequeño y que, alrededor de ésta, exista una frontera gravitacional a la cual llamamos horizonte de sucesos. El astrónomo y físico teórico alemán, Karl Schwarzschild, poco antes de su muerte en mayo de 1916, publicó "Acerca del campo gravitatorio de una masa puntual en el marco de la teoría de Einstein", la ecuación que da el tamaño de este horizonte de sucesos para cualquier cuerpo celeste, una magnitud conocida desde entonces como el radio de Schwarzschild:

R = 2 G M / C2

donde M es la masa del agujero negro, G es la constante gravitacional de Newton, y c2 es la velocidad de la luz. Así, el radio de Schwarzschild del Sol es de tres kilómetros, mientras el de la Tierra es de apenas un centímetro: si un cuerpo con la masa de la Tierra se comprimiera hasta el extremo de convertirse en una singularidad, la esfera (también puede tener otra forma) formada por su horizonte de sucesos tendría el modesto tamaño de una de las bolitas que usan los niños en sus juegos. Por otro lado, para una estrella de unas 10 veces la masa del Sol, el radio de Schwarzschild es de unos treinta kilómetros. Por otra parte, los acontecimientos que ocurren fuera del horizonte de sucesos en un agujero negro tienen un comportamiento como cualquier otro objeto cósmico de acuerdo a la masa que presente; por ejemplo, si el Sol se transformara en un agujero negro, la Tierra seguiría con los mismos patrones orbitales actuales.

Ahora bien, y en función de la fórmula anteriormente descrita, el horizonte de sucesos se incrementa en la medida que crece la masa del agujero. Existen evidencias observacionales que invitan a pensar que en muchos centros de galaxias se han formado ya agujeros negros supermasivos que han acumulado tanta masa (adsorciones de materia interestelar y estrellas) que su tamaño másico estaría bordeando sobre el millón de masas solares, pero su radio, el radio de Schwarzschild, no supera las 20 UA, mucho menor que nuestro sistema solar. Ello significa, para aclarar algunas especulaciones de ficción, que no existirían posibilidades de que un agujero negro pueda engullirse el universo completo.

Pese a la seguridad que hemos querido demostrar en lo poco que hemos descrito sobre la singularidad, siempre asalta la incertidumbre de que sea un tema bien comprendido por los lectores algo más lejanos de los quehaceres de la Física. En el pasado, no fue fácil su aceptación, a pesar de las radicales conclusiones que expuso Karl Schwarzschild en el artículo que hemos mencionado. Por mucho tiempo, no pasó de ser considerada como una curiosidad teórica. La comunidad científica no iba a valorar la trascendencia de sus implicaciones en la evolución estelar hasta que la Física de partículas y la astronomía acumularan medio siglo de conocimientos experimentales y de observaciones. En cualquier caso, el concepto mismo de singularidad desagradaba a muchos físicos, entre ellos al propio Einstein, pues la idea de una densidad infinita se alejaba de toda intuición. Nuestra naturaleza humana está mejor condicionada a percibir situaciones que se caractericen por su finitud, cosas que se puedan medir y pesar, y que se encuentren alojadas en unos límites concretos.

La noción de singularidad empezó a adquirir un mayor crédito cuando Robert Oppenheimer, junto con Hartland S. Snyder, en 1939, escribieron un artículo como anexo de otro que había escrito, el mismo año, Oppenheimer sobre las estrellas de neutrones. En este último artículo, describieron la conclusión de que una estrella con masa suficiente podía colapsarse bajo la acción de su propia gravedad hasta alcanzar un punto adimensional. Las ecuaciones descritas en el artículo del cual nos estamos refiriendo, demostraron de forma irrefutable que una estrella lo suficientemente grande continuaría comprimiéndose al final de su vida, más allá de los estadios de enana blanca y de estrella de neutrones, para convertirse en una singularidad. Los cálculos que realizaron Oppenheimer y Snyder para la cantidad de masa que debía tener una estrella para terminar sus días como una singularidad, estaban en los límites másicos de M= ~1 masa solar, estimación que fue corregida posteriormente por otros físicos teóricos que llegaron a la conclusión de que, para ser posible la transformación de una estrella en una singularidad, aquélla debe abandonar su fase de gigante roja con un núcleo residual con al menos 2 - 3 masas solares..

En su trabajo, Oppenheimer y Snyder desarrollaron el primer ejemplo explícito de una solución de las ecuaciones de Einstein que describe un agujero negro, al desarrollar el planteamiento de una nube de polvo colapsante. En su interior, existe una singularidad, pero no es visible desde el exterior, puesto que está rodeada por el horizonte de sucesos. Este horizonte es la superficie dentro de la cual los sucesos no pueden enviar señales hacia el Universo. Aparentemente, este modelo aparece como genérico, es decir, que representa el colapso gravitacional general. Pero, no obstante, sólo viene a representar una parte del tema, ya que el modelo OS posee una simetría especial (a saber, la simetría esférica) , pero para el caso de los agujeros negros es bastante descriptivo. El problema está en las dificultades que, por lo general, presentan las ecuaciones de Einstein para resolverlas. Por ello es que generalmente los teóricos, para este caso, buscan propiedades globales que involucren la existencia de singularidades.

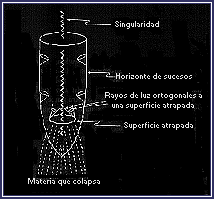
Modelo OS
La figura de la izquierda representa a la nube de polvo en colapso de Oppenhieimer y Snyder, que ilustra una superficie atrapada.
El modelo de Oppenhieimer y Snyder posee una superficie atrapada, que corresponde a una superficie cuya área se irá reduciendo a lo largo de los rayos de luz que son inicialmente ortogonales a ella.

Por ejemplo, se puede inferir, como lo hizo Roge Penrose en 1965, que la existencia de una superficie atrapada implica la existencia de una singularidad sobre la base de suposiciones razonables de casualidad, pero sin suponer una simetría esférica. O también se pueden concluir resultados semejantes suponiendo la existencia de un cono de luz convergente, como lo propugnaron el mismo Penrose, junto con Stephen Hawking en 1970, al afirmar que es posible que todos los rayos de luz emitidos en direcciones distintas desde un punto comienzan a converger más tarde entre sí.
También se pueden llegar a conclusiones, como lo hizo Stephen Hawking en 1965, en un estadio de tiempo revertido; o sea, en el contexto de una superficie atrapada revertida, lo que implica la existencia de una singularidad en el pasado (haciendo suposiciones de casualidad apropiada). Ahora, la superficie atrapada (en tiempo revertido) es muy extensa y se encuentra sólo dentro de una escala cosmológica.
Hemos afirmado que las singularidades se encuentran rodeadas por un horizonte de sucesos, pero para un observador, en esencia, no puede ver las singularidades mismas desde el exterior. Específicamente, implica que hay alguna región incapaz de enviar señales al exterior. La frontera de esta región es el horizonte de sucesos, en la cual tras ella se encuentra atrapado el pasado y el infinito nulo futuro. Lo anterior nos hace distinguir que esta frontera debería reunir las siguientes características:
En consecuencia, no es atrevido afirmar que se cuentan con variables para las singularidades. Efectivamente se dispone de ideas que poseen una similitud cualitativa con la solución de Oppenheimer y Snyder. Se introducen modificaciones, pero éstas son relativamente de menor importancia. Pero sí, su desarrollo se inserta mejor en el modelo de singularidad de Kerr, más que con el de Schwarzschild. Pero en general, el cuadro esencial es más bien similar.
Ahora bien, para que un ente, un objeto, o un observador pueda introducirse dentro de una singularidad como un agujero negro, en cualquiera de las formas que se dé, tendría que traspasar el radio de Schwarzschild (las fronteras matemáticas del horizonte de sucesos), cuya velocidad de escape es igual a la de la luz, aunque ésta tampoco puede salir de allí una vez atrapada dentro de los límites fronterizos determinados por el radio. En este caso, el radio de Schwarzschild puede ser calculado usándose la ecuación para la velocidad de escape.
Para el caso de fotones u objetos sin masa, se sustituye la velocidad de escape (vesc) por la de la luz c2, entonces el radio de Schwarzschild, R, es el conocido.

Estar cerca de una singularidad, aunque corresponda a un agujero negro pequeño (como el que se forma al colapsar una estrella) de unos pocos kilómetros de diámetro , teóricamente es bastante problemático. Las fuerzas de marea gravitatoria son, en las proximidades del agujero, enormes, y el aumento de la fuerza gravitatoria, incluso en una distancia de unos cuantos centímetros, es muy intensa. Si un agujero negro pasa a través de una nube de materia interestelar, o se encuentra cerca de una estrella normal, la fuerza gravitatoria de éste atrae materia hacia su interior. Como la materia cae hacia el agujero negro, desarrolla energía cinética que al calentarse por las fuerzas de mareas gravitatorias ioniza los átomos que están siendo atrapados, y estos, cuando alcanzan algunos millones de grados Kelvin, emiten rayos X. Estos rayos X son remitidos hacia el espacio exterior antes que la materia traspase la frontera del horizonte de sucesos y sea engullida por la singularidad que es un agujero negro. Observar la emisiones de rayos X es uno de los medios para rastrear el cosmos tras la caza de un agujero negro.
Pese a que para muchos, lo anteriormente descrito no va más allá de fascinantes novedades teóricas, sin embargo, los agujeros negros, como singularidades de una teoría, dejaron de ser meras especulaciones matemáticas, pasando a ocupar el centro de la astronomía especulativa. La mayoría de los físicos se encuentran convencidos que tienen que existir, pero aún no se disponen de suficientes pruebas observacionales concluyentes que confirmen la previsión teórica, pese a la ya importante cantidad de muestras que ya se han observado sobre objetos y materias cuyo comportamiento reúne todas las características de encontrarse en una ubicación cercana a "algo" de un gran poder gravitacional. Seguramente, nunca podremos tocar o ver a una singularidad como un agujero negro, claro está, pero podemos distinguir señas identificatorias observables y, al final, la fuerza de los hechos nos convencerán que allí están.
Por otra parte, si aceptamos que las leyes de la Física son simétricas en el tiempo y hemos deducido la existencia de objetos llamados agujeros negros donde caen cosas que no pueden salir, por qué no considerar, como ya lo han pensado varios teóricos, entre ellos Stephen Hawking, la existencia de otro tipo de objetos de donde las cosas puedan salir pero no caer. Cabría denominarlos «agujeros blancos». Se podría imaginar a un astronauta saltar a un agujero negro en algún lugar para salir en otro por un agujero blanco. Sería un método ideal para los viajes espaciales a largas distancias. Claro está, que primero sería necesario resolver la cuestión de cómo introducirse en un agujero negro sin antes ser despedazado por las tremendas fuerzas de mareas gravitatorias que se dan aledañas al agujero.

EL CENSOR CÓSMICO

El físico-matemático inglés Roger Penrose demostró en 1965 que todos los agujeros negros contienen una singularidad. Pero quedó tan consternado ante la idea de una «singularidad desnuda» que propuso la idea de la existencia de un «censor cósmico» encargado de asegurar que las singularidades estén decentemente "vestidas" con un horizonte de sucesos. De esta forma, las singularidades estarían separadas de nuestro universo. Pero, pese a su reconocida voluntad de trabajo investigativo, Penrose no ha demostrado que el censor cósmico exista, y otros físicos piensan que las singularidades desnudas pueden existir, aunque sea solo durante un tiempo muy limitado.

Al final de la década de los sesenta, los científicos que investigaban los agujeros negros se dieron cuenta de una posibilidad matemática, que si bien cuenta con ecuaciones consistentes, si se diera en la praxis mecánica del cosmos debería ser considerada como tétrica. Cuando una estrella como un agujero negro se forma, un horizonte de sucesos esconde la singularidad. Pero en determinados escenarios matemáticos, se puede llegar a formar un agujero negro sin horizonte de sucesos. Si eso sucediera en el universo, entonces sería posible ver la singularidad y tal vez, incluso, entrar y volver a salir de ella. Pero las singularidades son lugares de densidad infinita en las que las leyes de la Física no funcionan y en donde puede suceder cualquier cosa. Y, sin horizontes de sucesos, no hay nada que proteja a la porción de universo que circunda los agujeros negros: allí regiría la anarquía cósmica. Sin embargo, si se dieran las «singularidades desnudas», podrían ser un objetivo irresistible para los futuros tripulantes de las naves intergalácticas semejantes a las descritas por los escritores de ciencia ficción contemporáneos.
Resumiendo, una singularidad es el triunfo final de la fuerza de gravedad, es la compresión de la materia hasta llevarla a tener una densidad infinita. Si la estrella o el objeto que sufre la compresión no gira, la gravedad comprime la materia de forma simétrica. El resultado de la singularidad es un punto infinitamente pequeño (abajo, izquierda). Si el objeto que sufre la compresión gira, las fuerzas de rotación lo ensanchan y éste adquiere la forma de un anillo. Este se encoge, formándose un anillo infinitesimalmente delgado (abajo, derecha).

                                                                                                                                                   © 2000 Javier de Lucas