LA TEORIA DINEMO

Trataremos aquí de describir los fundamentos de una de las alternativas teóricas que se barajan, dentro del mundo de la Física, para explicarnos las razones del comportamiento que observamos del radio de curvatura de las galaxias, en el evento que las investigaciones que se están llevando acabo sobre la estructura de los halos galácticos determinen que éstos no comportan cantidades importantes de materia como para que su efecto sea el que se refleja en los gráficos que demuestran ese radio de curvatura.
Este es un tema que no solamente compromete a la hipótesis sobre los halos galácticos de materia oscura, sino que también a leyes fundamentales de la Física. De llegar a comprobarse observacionalmente que los halos de las galaxias no son los agentes determinantes del comportamiento del radio de curvatura de estos astros, no sólo se compromete a la hipótesis sobre la materia oscura, sino que también a otras y, lo que más preocupa, a leyes fundamentales de la Física. De suceder esto último, algunos científicos ya han colocado sobre la mesa teorías e ideas alternativas que pueden suplir las dificultades que puedan experimentar esas leyes. Una de esas teorías es la denominada "Dinámica Newtoniana Modificada" (DINEMO) o "Modified Newtonian Dynamics" (MOND).
La DINEMO, aparecida en el año 1983, fue presentada por su autor, el físico israelita Mordehai Milgrom, en el Astrophysical Journal. Esencialmente, promueve las curvas de rotación plana y las leyes astrofísicas de la materia oscura. En ella, Milgrom propugna la introducción, dentro del marco de una ley fundamental de la Física, de una nueva constante medular, a0, con dimensiones de aceleración, y cuyo valor es 2 x 10-8 cm. s-2.
Una sencilla forma de explicar, entre otras, los rasgos descriptivos de la DINEMO, es el enunciado que dice que la masa inercial de un objeto depende de la intensidad del campo al cual está sometido. Una estrella que está a gran distancia del centro de una galaxia está inmersa en un campo gravitacional débil; así su masa inercial es más pequeña, y cuesta menos acelerarla para mantenerla en órbita. De esta manera podemos tener curvas de rotación planas sin invocar cantidades enormes de materia. Aquí, las objeciones que se le hicieron por parte de Yabushita y Fenzi, no son procedentes, pues no se cambia la ley de fuerza. Más importante aún, todas las propiedades de sistemas extragalácticos quedan salvaguardadas y encuentran una explicación natural.
La sucinta descripción expuesta sobre la DINEMO, que obedece a una, entre otras, de sus posibles interpretaciones, en alguna medida se adhiere con el principio de Mach; también lo es la coincidencia entre los valores de a0 y cH0 y entre a0G-1 y las densidades de masa «superficial» máxima de galaxias (leyes de Freeman y de Fish en su versión moderna).
Esta teoría de Milgrom no es muy popular y está lejos de ser aceptada por la comunidad científica, pero a raíz de los avances en los trabajos de búsqueda de materia oscura en los halos de las galaxias, muchos de los integrantes de los diferentes equipos dedicados a la investigación de este tema, la han retomado para observar su posibilidad en diferentes escenarios. La falta de aceptación generada hasta ahora por la teoría, se debe, principalmente, a no haber sido posible, hasta la fecha, colocarla en un marco matemático autoconsistente y elegante con el mismo rango de acción que la Relatividad General. Ello, pese a que algunos de los problemas de la versión original desaparecieron con nuevas formulaciones que le introdujeron Bekenstein y el mismo Milgrom, en el año 1984. Pero tiene dificultades con casualidad (palabra que en este caso se refiere a la posible existencia de señales que se propaguen a velocidades mayores que la de la luz, que en el contexto de la Teoría Especial de la Relatividad da lugar a un gran número de paradojas). Sin embargo, lo anterior no impide hacer cosmología con esta teoría.
Uno de los problemas serios con que se enfrenta la DINEMO, es su profunda incompatibilidad con la Teoría General de la Relatividad (TGR). Uno de los principios medulares de la TGR es el llamado Principio de Equivalencia Fuerte (PEF), que enuncia que la masa inercial y la masa gravitacional de un objeto son exactamente iguales. Una vez descrito este principio se llega a la TGR de Einstein casi sin esfuerzo. Como se extrae del enunciado que ya describimos sobre la DINEMO, ésta requiere que la masa inercial, y no la masa gravitacional, dependa de la intensidad del campo a la que está sometida (o a la aceleración); DINEMO no satisface el PEF. En su lugar, satisface a lo que se llama Principio de Equivalencia Débil (PED). El PED, sólo dice que estas masas son proporcionales. Las evidencias experimentales sólo avalan el PED. El PEF viene a ser justificado casi exclusivamente por los éxitos que ha logrado la TGR en su contexto general.
Las evidencias observacionales que dan cabida a la DINEMO (sin consecuencias precisas para TGR) tienen que ver con la dinámica de los cúmulos estelares galácticos. Los campos gravitacionales dentro de estos cúmulos son muy débiles, lo que indicaría que las diferencias entre las predicciones de la DINEMO y TGR serían importantes. Cuando estudiamos estos objetos encontramos que no muestran evidencia de materia invisible u oscura, lo que estaría colocando en dificultades aplicativas a la DINEMO; pero, sin embargo, al encontrarse estos objetos en el campo gravitacional de nuestra galaxia, hace que las masas inerciales tengan los valores usuales, lo que hace que las predicciones de la DINEMO con las de la TGR coincidan. Este efecto, que la dinámica interna de un sistema dependa del campo en el que el sistema está cayendo, aunque éste sea constante (sus efectos de mareas son despreciables), viene a ser una transgresión sustancial del PEF. Pero es necesario subrayar que eso ocurre sólo dentro del marco previsto por DINEMO; para la TGR estos objetos no contendrían materia invisible u oscura.
Por otra parte, la DINEMO y la teoría de Newton con materia invisible u oscura pueden llegar a ser complementarias. Pero, eso sí, debemos comparar las predicciones de cada teoría como se encuentran en la actualidad formuladas, con las observaciones que puedan caber. Ahora bien, si se encuentran discrepancias significativas, esto no debe necesariamente implicar la destrucción de su esencia medular, sino más bien necesidades de algunos aspectos de reformulación. Es necesario considerar un espacio de tiempo lo suficientemente necesario para que la nueva teoría tenga la ocasión de poder refinarse, y a la antigua, por su condición meritoria de protegerse. Será necesario que el tiempo determine cual es la teoría que está evolucionando positivamente, aunque ello sea considerado poco consistente, pero que adquiere ribetes importantes cuando se observan ejemplos del pasado (e.g. éter y relatividad, física aristotélica y galiliana, etc.).
Pero lo importante es, en el fondo, el contar con herramientas teóricas para coadyuvarnos a encontrar respuestas sustentables para materias que aún no se encuentran sustanciales explicaciones. Para que la hipótesis de la materia invisible u oscura no pierda su rango de científica, está el hecho de que no podemos agregar masa a una galaxia impunemente. El físico pakistaní, con una gran parte de formación autodidacta y premio Nobel de Física en 1983, Subramanyan Chandrasekhar, en el año 1939 publicó un libro que tituló "Una introducción al estudio a la estructura estelar", y en él propugna y demuestra que un objeto masivo, moviéndose entre un grupo de otros objetos masivos, sufre un frenado, una desaceleración de naturaleza dinámica: al moverse este objeto, su masa afecta la trayectoria de los otros que lo rodean, creando una «estela» de exceso de masa tras él; esta estela masiva ejerce una fuerza gravitacional en el objeto que la creó, la que se llama fricción dinámica. Esta fuerza da lugar a una desaceleración cuya magnitud es proporcional a la masa del objeto que está siendo desacelerado. En otras palabras, aquellos objetos más masivos terminarán moviéndose más lentamente.
El efecto que hemos descrito anteriormente es tan importante que, cuando se hicieron las primeras simulaciones de cúmulos de galaxias, en la que se dividió la masa observada típica de cúmulos entre las galaxias que lo componen, no sólo se desarrolló un grado altísimo de segregación de masa, debido a que las galaxias más pesadas se hundían rápidamente hacia el centro del cúmulo, sino que todas las galaxias se desaceleraban rápidamente cayendo hacia el centro del cúmulo, provocando su rápido colapso. Fue esto último lo que invitó a los investigadores a asumir que la mayor parte de la masa de los cúmulos estaba asociada a un medio intergaláctico, y no a las galaxias. Así se logró disminuir la masa de las galaxias, reduciendo consecuentemente la magnitud de la aceleración de Chandrasekhar. Eso fue hecho en forma, digamos, casi sutil, no tanto como para proteger a la teoría newtoniana, sino que más bien para dar explicaciones a las observaciones. Sin embargo, trajo importantes implicaciones; la más directa de ellas fue eliminar efectivamente el proceso de fricción dinámica como un factor importante en la evolución de los cúmulos de galaxias. Es muy probable que el resultado de esto sea nuestra incapacidad de explicar, entre otras cosas, la formación de las galaxias elípticas, y en especial ese tipo de galaxias gigantes llamadas cD que habitan los centros de los cúmulos.
No deja de ser una sorpresa encontrar hoy, después de veinte años transcurrido desde las escenas de esas simulaciones, a físicos que siguen redescubriendo que la fricción dinámica no es lo suficientemente fuerte para formar la estructura total de los cúmulos de las galaxias; pero soslayan el hecho de que ésta, en alguna medida, fue «archivada» su participación por los mismos teóricos investigadores, cuando desarrollaron la teorización de la formación de los cúmulos. Las propiedades de estos objetos son, generalmente, atribuidas a complejos procesos físicos que se dieron en los comienzos de su formación .
El soslayar la importancia del efecto de la fricción dinámica en el proceso de la formación y evolución de las galaxias y de los cúmulos, se debe a la carencia de evidencias observacionales de segregación de masa en estos tipos de objetos, que es la principal característica que identifica a esta clase de fricciones. Sin embargo, se viene observando ciertos cambios en algunos teóricos para considerar en otro rango de importancia los efectos de la fricción dinámica, usando para ello la recreación científica de teorías que entreguen otras posibilidades de interpretación a ciertos fenómenos que reiterativamente han sido detectados por la observación. Uno de estos casos se da en lo que ha venido ocurriendo, en los últimos tiempos, con la Teoría DINEMO. En las recreaciones que se han hecho de ella, se estaría llegando a la conclusión que la DINEMO sería capaz de predecir una fricción análoga a la que descubrió Chandrasekhar para la teoría de Newton, pero con la variante en que la desaceleración es independiente de la masa del objeto: fricción dinámica sin segregación de masa.
Las conclusiones preliminares a las que estarían llegando los físicos teóricos que se encuentran abocados, actualmente, a la recreación científica de la DINEMO, es que ésta comportaría la capacidad de explicar, entre otras cosas, la formación de galaxias cD, la distribución de cúmulos globulares alrededor de galaxias y el origen de la fuente de energía del gas que emite rayos-X en cúmulos de galaxias. Pero además, nace otra perspectiva en cuanto a que emerja una nueva percepción del Cosmos a escalas galácticas y mayores, donde la fricción dinámica juegue un papel mucho más importante que el hasta ahora se le ha asignado, quizás hasta el hecho que se le pueda reconocer como el principio palanca de la evolución.
Dentro de las varias observaciones que dieron pie para que muchos teóricos consideraran la posibilidad de retomar a la DINEMO, tienen relación con lo que se llama función de correlación de 2-puntos de la distribución de galaxias. Para explicar el significado de lo anterior, podemos describir sucintamente lo siguiente: la presencia de una galaxia en un punto del espacio indica que otra no puede estar lejana, lo que se asemeja a varias analogías comunes que la humanidad observa diariamente, como es el caso de las gaviotas en el mar con respecto a una señal de tierra cercana. La función de correlación de 2-puntos es una medida de la probabilidad de encontrar una galaxia a una distancia determinada de otra. Es una función porque depende de la distancia. Su valor decrece con la distancia. La forma exacta de esta función ha sido determinada para un gran rango de separaciones y es la misma para grandes distancias (millones de años luz) como para pequeñas distancias (miles de años luz).
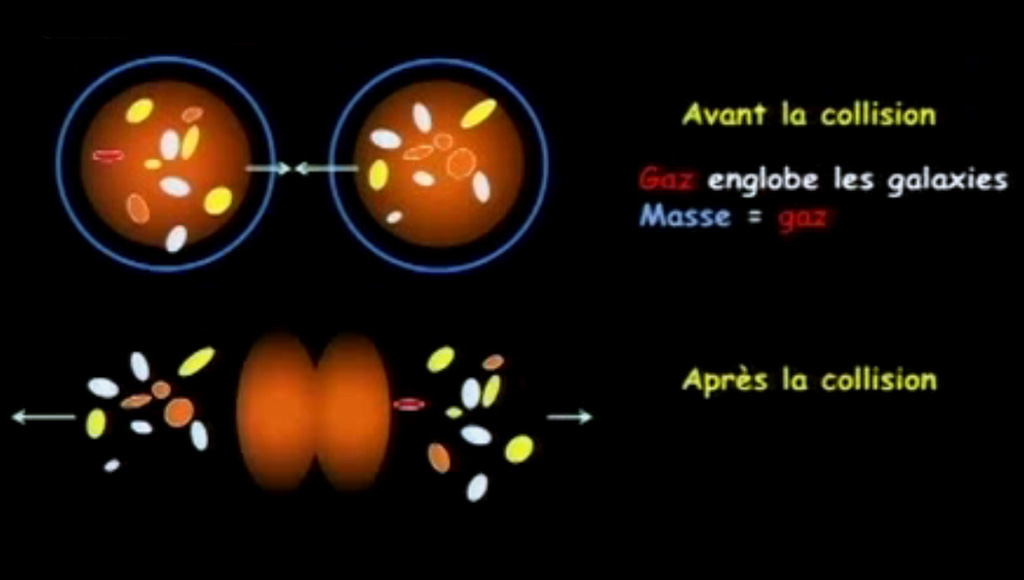
Lo inmediatamente anterior, siempre no ha dejado de sorprender a los estudiosos la estructura observable del cosmos. Los halos de materia oscura debieran trasladarse dando lugar a los que se llaman "merging", la rápida unión de las dos galaxias involucradas en un proceso doble donde la fricción dinámica las desacelera y acerca, para luego unirse éstas en un choque inelástico, donde gran parte de la energía orbital de las galaxias es traspasada a energía interna (movimiento de las estrellas que la componen). Se esperaba que esto diera lugar a un cambio en la función de correlación a las distancia en los cuales los halos comienzan a trasladarse (aproximadamente el doble del tamaño típico de estos halos). Sin embargo, ningún cambio ha sido detectado, ya que esta función mantiene el mismo comportamiento hasta distancias del orden de los 15.000 años luz, aunque recientemente existen algunas evidencias observacionales que habrían detectado algunos cambios, pero a distancias que corresponderían a los traslados de las partes visibles de las galaxias, lo que se estimaría en aproximadamente unos 30.000 años luz.
Pero esto no es todo. Quizás sea más relevante lo que se obtiene en el proceso que lleva a la unión de dos galaxias, que no es otro que la fricción dinámica, donde se esperaba detectar segregación de masa en la función de correlación a distancias pequeñas, lo que no ha sido evidenciado. Dentro del marco de la DINEMO, estos dos hechos observacionales son naturalmente explicados, ya que en él, los halos de materia oscura no requieren cantidades enormes de material coexistiendo en ellos, como lo demanda la teoría clásica newtoniana. Pero, sin embargo, dentro de cualquiera de las circunstancias, las necesidades de conocer tanto los tamaños como estructuras de estos halos, siempre adquiere ribetes de excepción. Señalo lo anterior, pese a que las observaciones de sistemas de galaxias binarios indican que estos halos son del orden de 180.000 años luz o más, lo que estaría poniendo a la hipótesis de la existencia de la materia oscura en algunas dificultades, pero hay escenarios computacionales donde se ha expuesto este problema, que estarían desestimando esa posibilidad.
Es muy probable que no tengamos mucho que esperar para saber qué teoría sería la que explicaría el comportamiento observacional de las galaxias. Si éstas aparentaran tener halos masivos con extensiones mayores que aproximadamente 40 kpc. la Teoría Newtoniana se pondría en aprietos, lo que deseamos muchos que no sea así. De todas maneras debemos esperar y evitar algunas de nuestras tendencias a parecernos a nuevos y «sólidos» iconoclastas científicos que con tanta profusidad aparecen en ocasiones, cuando los propios militantes de las comunidades científicas difunden partes de sus trabajos teóricos. Hasta ahora, siguen en plena vigencia y esplendor nuestras clásicas leyes de la Física.
Es cierto que aquellos estudiosos de las problemáticas de la Física se encuentran, hoy día, en una disyuntiva bastante peculiar. Por un lado, se tiene dinámica newtoniana más materia oscura con base en una teoría matemáticamente elegante y físicamente completa, pero que al ser aplicada a sistemas astrofísicos no satisface las necesidades de explicación sobre sus propiedades básicas. Esto no podría sorprendernos si se logra determinar que esas propiedades no pueden ser explicadas por las leyes newtonianas de la Física. Por otra parte, se cuenta con la DINEMO, que no deja de ser una teoría ingeniosa y, a su vez, sorprendente, y que nos puede ayudar a explicarnos el comportamiento de esos sistemas. Pero también se debe reconocer que no se caracteriza por su elegancia y la amplitud de su margen de aplicación al entendimiento de los fenómenos que a la Física se le ha requerido explicar.
La evolución que ha alcanzado la humanidad reclama de pensadores, profesionales y científicos que estén abocados a asumir la decisión de tomar una determinación. Aparece, casi como si fuera lo único constante, el cambio. En las Ciencias, es difícil contemplar el aferrarse a ideas y paradigmas de eterna duración. El trabajo de Milgrom, no deja de ser inteligente y también, por qué no decirlo, de gran osadía. Viene a ser una muestra del comportamiento actual del hombre moderno de Ciencias, pero que en ningún caso viene a corresponder a una identidad tipo iconoclasta. Se ha llegado a una etapa de desarrollo científico en la cual tanto físicos como astrónomos se encuentran emplazados a moverse dentro de laberintos y estar expuestos a los embates de los caminos de la incertidumbre. Si no se detecta suficiente materia oscura en los halos galácticos para que su comportamiento pueda ser explicado con rigor por las leyes de Newton, entonces se deberá recurrir a otras teorías, como la DINEMO, para someterla, con el debido rigor que se requiere, al hecho de que sean capaces de explicarnos fenómenos que, con los instrumentos clásicos, no se pudo encontrar respuestas satisfactorias.
Precisemos, primero, lo que respecta a las bases del movimiento circular. Para este proceso podemos recurrir a un ejemplo. Imaginémonos que tomamos una plomada, y la hacemos girar por encima de nuestra cabeza. Los parámetros que tenemos en este sistema son: la masa del peso o plomo; el radio de giro del hilo que une nuestras manos con la punta del peso, y la rapidez (valor absoluto de la velocidad) que es constante. A mayor rapidez el peso o plomo parece generar un tirón con más fuerza. Este es un efecto de la Segunda Ley de Newton que dice que la fuerza que ejerce el peso en el hilo es igual a su masa inercial (definida por esta ley) multiplicada por la aceleración. Esta propiedad, la masa inercial, de antemano, no tiene relación con la gravedad. Un astronauta en una nave espacial en órbita alrededor de la Tierra, en cuyo lugar los efectos de la gravedad terrestre son anulados por la caída libre que provoca el movimiento orbital, el hacer girar la misma plomada surtirá el mismo efecto de tirón que se percibe en el mismo ejercicio efectuado en la Tierra. De este modo, la masa inercial aparece como una propiedad intrínseca del objeto, con independencia de su peso.
La fuerza que ejerce el peso en el hilo es también proporcional a la aceleración, que para un movimiento circular con velocidad constante está dada por el cuadrado de la velocidad dividido por el radio de giro: al doble de la velocidad, la aceleración y la fuerza del tirón de la plomada, se cuadruplican. Si se reduce el radio de giro a la mitad, la aceleración y la fuerza se duplican. Esto también sucede en el movimiento de una estrella en una galaxia si asociamos la tensión en el hilo de la plomada con la fuerza de atracción que ejerce la propia galaxia sobre la estrella. Mientras más masiva es la galaxia, mayor es la fuerza y más rápido es el giro de la estrella entorno a la galaxia.
Isaac Newton no sólo es el responsable de la famosa Segunda Ley de la Dinámica, en la cual introduce el concepto de masa inercial, sino que también de esa maravillosa interpretación de una de las características que comporta la Naturaleza en la cual habitamos, que es la Ley de Gravitación Universal, en la cual introduce el concepto de masa gravitacional. Newton, en el proceso que siguió para desarrollar estas leyes, utilizó lo que se conoce como experimento del pensamiento: utilizar un escenario imaginario para iluminar las reglas que gobiernan el mundo real. Este procedimiento es una herramienta indispensable para los científicos en todos los campos, pero en especial para los cosmólogos, cuyas teorías son a menudo imposibles de comprobar. Sin embargo, Newton tenía a su disposición una herramienta poderosa que le permitía llegar a conclusiones acertadas: las Matemáticas. Con ellas, podía recorrer largos caminos hacia confirmar su hipótesis de la gravedad calculando sus consecuencias y luego comparando sus resultados con las experiencias observacionales. Pero primero, tenía que formular una expresión exacta de las relaciones entre la fuerza gravitatoria, la masa y la distancia.
Newton supuso que la fuerza del tirón gravitatorio de un objeto es directamente proporcional a su masa, considerándose para esos efectos las características de ésta como una propiedad a la que se denomina masa gravitacional, la cual hace que los objetos se atraigan con una fuerza proporcional al producto de estas masas, e inversamente proporcional al cuadrado de la distancia que los separa. Este es uno de los descubrimientos más notable que aportó Newton a la Física.
Al enunciar su Segunda Ley, fuerza igual a masa inercial multiplicada por la aceleración, la masa inercial se cancela con la masa gravitacional que aparece en la fuerza (se asume sólo fuerza gravitacional), dejando la constante de proporcionalidad que relaciona ambos tipos de masas, lo que implica concluir que la aceleración, y por consiguiente el movimiento, es independiente de la masa del objeto. Esto se conoce como el Principio de Equivalencia Débil (PED). Pero Einstein fue más lejos y propuso lo que se llama Principio de Equivalencia Fuerte (PEF), cuyo enunciado señala que la masa inercial es exactamente igual a la masa gravitacional (la constante de proporcionalidad es exactamente igual a 1). Por otra parte, la Teoría DINEMO propugna que esta «constante» de proporcionalidad es una función de la aceleración (o intensidad de campo) a la que está sometida la masa. Para grandes aceleraciones esta función tiende a 1. Para aceleraciones bajas esta "constante" es proporcional a la aceleración, o sea, es una función lineal de la aceleración.
Al multiplicar la masa por una función que en los límites de aceleraciones pequeñas es proporcional a la aceleración, resulta importante dividir, al mismo tiempo, por una cantidad con dimensiones de aceleración, con el objeto de preservar las dimensiones de masa. Esta cantidad a0, entra entonces en la Teoría DINEMO como una constante fundamental que simultáneamente define qué queremos decir cuando hablamos de aceleraciones grandes o pequeñas. El valor numérico de esta constante ha sido medido analizando las curvas de rotación de galaxias espirales. y está dado por:
a0 ~ 2 x 10-8cm/s2
Para mayores aceleraciones que a0 se retoma la teoría de Newton. Para aceleraciones mucho menores se está en lo que se llama régimen microdinámico. Volviendo al movimiento de estrellas en una galaxia, éstas pueden considerarse en el régimen microdinámico; así la masa inercial de estas estrellas decrece a medida que nos alejamos del centro de la galaxia, haciéndose menor la fuerza necesaria para mantenerla en órbita a las altas velocidades implicadas por la curva de rotación plana. La teoría de Newton requiere aumentar la fuerza, lo que hace introducir más masa, y esto implica la necesidad de una composición mayor de materia: la que se presume encontrar en los halos galácticos.
© 2006 Javier de Lucas