Dinámica |
Colisiones Carro que dispara un proyectil Caída libre y sucesivos rebotes
Choques frontales Choques frontales elásticos Choques frontales verticales Choque inelástico de duración finita Péndulo balístico No se conserva el momento lineal Choque entre una partícula y un bloque unido a un muelle Medida de la veloci- dad de una bala Choques bidimen sionales Conservación del momento lineal |
||||
|
En esta página, se estudia el choque de dos esferas iguales que cuelgan de sendos hilos inextensibles y de masa despreciable. Las esferas se separan de su posición de equilibrio, ángulos iguales, se sueltan y se observa cómo decae la amplitud de sus oscilaciones como consecuencia de los choques.
Fundamentos físicosMovimiento de las esferas
Para determinar la posición angular θ de cada péndulo (el ángulo que forma con la vertical) en función del tiempo, se resuelve la ecuación diferencial por procedimientos numéricos en dos etapas con las siguientes condiciones iniciales:
Balance energéticoComparemos dos posiciones del péndulo:
La energía se conserva v2=2gl(cosθ-cosθ0) La velocidad u de cada una de las esferas justamente antes del choque, cuando θ=0 es u2=2gl(1-cosθ0) Choque de dos esferas
Las velocidades de las esferas v1=-v y v2=v después del choque están relacionadas con las velocidades u1=u y u2=-u antes del choque mediante v1-v2=-e(u1-u2) La velocidad v de las esferas después del choque disminuye ya que el coeficiente de restitución e<1. v=e·u
Sucesivos choques de las dos esferasEn la figura, se muestra:
|
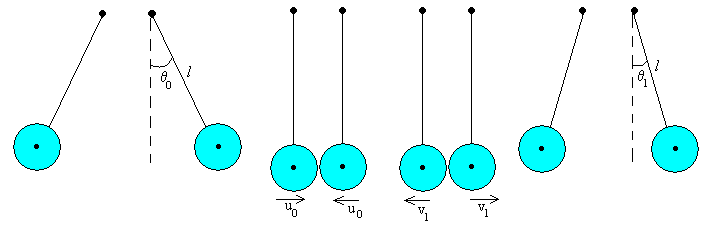
Balance energéticoA medida que las esferas chocan su energía va disminuyendo. La energía inicial de cada una de las esferas es E0=mg(l-l·cosθ0) Después de n choques la energía de cada una de las esferas es En=mg(l-l·cosθn)=mgl·e2n·(1-cosθ0)
EjemploSe desvía cada una de las esferas un ángulo de θ0=90º de la posición de equilibrio En el siguiente cuadro, se especifica la máxima desviación θn, la proyección en dicha posición xn del centro de la esfera sobre el eje X, y la energía En.
ActividadesSe introduce
Se pulsa el botón titulado Empieza Se observa el movimiento de las dos esferas idénticas que parten de la posición θ0=90º y a continuación se sueltan. Las esferas se acercan, chocan, se alejan hasta que alcanzan la desviación máxima y así, sucesivamente. Sobre el eje horizontal, se van marcando las proyecciones del centro de una de las esferas cuando alcanzan la desviación máxima. En la parte izquierda del applet, se muestra el balance energético:
En la parte superior del applet se proporcionan los datos de
|
||||||||||||||||||||||||||